
题目列表(包括答案和解析)
4.若方程x2+(k-2)x+2k-1=0的两根中,一根在0和1之间,另一根在1和2之间,求实数k的取值范围.
[解析] 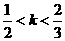 ;令
;令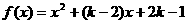 ,则依题意得
,则依题意得
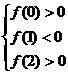 ,即
,即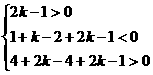 ,解得
,解得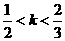
3.已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若在区间[-1,1]内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________.
[解析] (-3,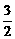 ) 只需f(1)=-2p2-3p+9>0或f(-1)=-2p2+p+1>0
) 只需f(1)=-2p2-3p+9>0或f(-1)=-2p2+p+1>0
即-3<p<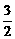 或-
或-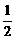 <p<1.∴p∈(-3,
<p<1.∴p∈(-3, 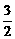 ).
).
3.用二分法研究函数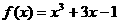 的零点时,第一次经计算
的零点时,第一次经计算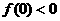 ,
,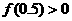 ,可得其中一个零点
,可得其中一个零点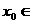 ,第二次应计算
,这时可判断
,第二次应计算
,这时可判断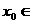
[解析] 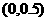 ,
,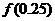 ,
,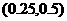 ;由二分法知
;由二分法知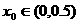 ,这时
,这时
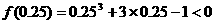 ,故
,故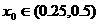
考点3 根的分布问题
[例4] 已知函数f(x)=mx2+(m-3)x+1的图像与x轴的交点至少有一个在原点的右侧,求实数m的取值范围
[解题思路]由于二次函数的图象可能与x轴有两个不同的交点,应分情况讨论
[解析](1)若m=0,则f(x)=-3x+1,显然满足要求.
(2)若m≠0,有两种情况:
原点的两侧各有一个,则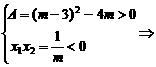 m<0;
m<0;
都在原点右侧,则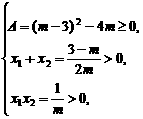
解得0<m≤1,综上可得m∈(-∞,1].
[名师指引]二次方程根的分布是高考的重点和热点,需要熟练掌握有关二次方程ax2+bx+c=0(a≠0)的根的分布有关的结论:
①方程f(x)=0的两根中一根比r大,另一根比r小 a·f(r)<0.
a·f(r)<0.
②二次方程f(x)=0的两根都大于r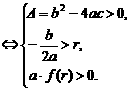
③二次方程f(x)=0在区间(p,q)内有两根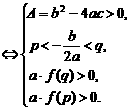
④二次方程f(x)=0在区间(p,q)内只有一根 f(p)·f(q)<0,或f(p)=0,另一根在(p,q)内或f(q)=0,另一根在(p,q)内.
f(p)·f(q)<0,或f(p)=0,另一根在(p,q)内或f(q)=0,另一根在(p,q)内.
⑤方程f(x)=0的两根中一根大于p,另一根小于q(p<q)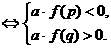
[新题导练]
2.(中山市09届统测)方程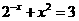 的实数解的个数为 _______
的实数解的个数为 _______
[解析] 2;在同一个坐标系中作函数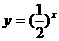 及
及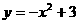 的图象,发现它们有两个交点
的图象,发现它们有两个交点
故方程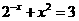 的实数解的个数为2
的实数解的个数为2
考点2 用二分法求方程的近似解
[例4](斗门一中09届模拟)利用计算器,列出自变量和函数值的对应值如下表:
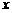 |
0.2 |
0.6 |
1.0 |
1.4 |
1.8 |
2.2 |
2.6 |
3.0 |
3.4 |
… |
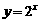 |
1.149 |
1.516 |
2.0 |
2.639 |
3.482 |
4.595 |
6.063 |
8.0 |
10.556 |
… |
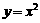 |
0.04 |
0.36 |
1.0 |
1.96 |
3.24 |
4.84 |
6.76 |
9.0 |
11.56 |
… |
那么方程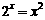 的一个根位于下列区间的( ).
的一个根位于下列区间的( ).
A.(0.6,1.0);B.(1.4,1.8);C.(1.8,2.2);D. (2.6,3.0)
[解题思路]判断函数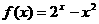 在各个区间两端点的符号
在各个区间两端点的符号
[解析]由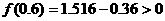 ,
,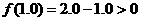 ,故排除A;
,故排除A;
由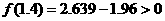 ,
,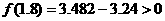 ,故排除B;
,故排除B;
由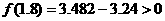 ,
,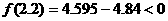 ,故可确定方程
,故可确定方程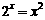 的一个根位于下列区间(1.8,2.2),所以选择C
的一个根位于下列区间(1.8,2.2),所以选择C
[名师指引]用二分法求方程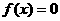 的近似解的关键是先寻找使得函数
的近似解的关键是先寻找使得函数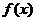 在两端点异号的某区间,然后依次取其中点,判断函数
在两端点异号的某区间,然后依次取其中点,判断函数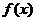 在中点的符号,接着取两端函数值异号的区间作为新的区间,依次进行下去,就可以找到符合条件的近似解。
在中点的符号,接着取两端函数值异号的区间作为新的区间,依次进行下去,就可以找到符合条件的近似解。
[新题导练]
1.(09年浙江五校联考)函数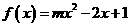 有且仅有一个正实数的零点,则实数
有且仅有一个正实数的零点,则实数 的取值范围是( )
的取值范围是( )
A.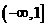 ;B.
;B.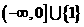 ;C.
;C. ;D.
;D.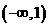
[解析] B;依题意得(1)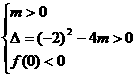 或(2)
或(2)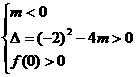 或
或
(3)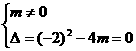
显然(1)无解;解(2)得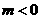 ;解(3)得
;解(3)得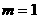
又当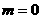 时
时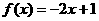 ,它显然有一个正实数的零点,所以应选B
,它显然有一个正实数的零点,所以应选B
3.关于用二分法求函数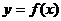 的零点近似值的步骤须注意的问题:
的零点近似值的步骤须注意的问题:
(1)第一步中要使:①区间长度尽量小;②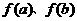 的值比较容易计算且
的值比较容易计算且
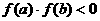 ;
;
(2)根据函数的零点与相应方程根的关系,求函数的零点与求相应方程根是等价的。对于求方程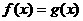 的根,可以构造函数
的根,可以构造函数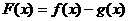 ,函数
,函数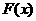 的零点即方程
的零点即方程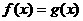 的根。
的根。
★热点考点题型探析
考点1 零点的求法及零点的个数
题型1:求函数的零点.
[例1] 求函数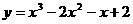 的零点.
的零点.
[解题思路]求函数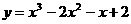 的零点就是求方程
的零点就是求方程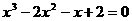 的根
的根
[解析]令 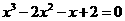 ,∴
,∴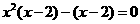
∴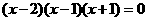 ,∴
,∴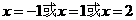
即函数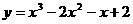 的零点为-1,1,2。
的零点为-1,1,2。
[名师指引] 函数的零点不是点,而是函数函数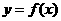 的图像与x轴交点的横坐标,即零点是一个实数。
的图像与x轴交点的横坐标,即零点是一个实数。
题型2:确定函数零点的个数.
[例2] 求函数f(x)=lnx+2x -6的零点个数.
[解题思路]求函数f(x)=lnx+2x -6的零点个数就是求方程lnx+2x -6=0的解的个数
[解析]方法一:易证f(x)= lnx+2x -6在定义域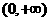 上连续单调递增,
上连续单调递增,
又有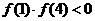 ,所以函数f(x)= lnx+2x -6只有一个零点。
,所以函数f(x)= lnx+2x -6只有一个零点。
方法二:求函数f(x)=lnx+2x -6的零点个数即是求方程lnx+2x -6=0的解的个数
即求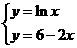 的交点的个数。画图可知只有一个。
的交点的个数。画图可知只有一个。
[名师指引]求函数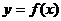 的零点是高考的热点,有两种常用方法:
的零点是高考的热点,有两种常用方法:
①(代数法)求方程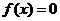 的实数根;
的实数根;
②(几何法)对于不能用求根公式的方程,可以将它与函数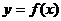 的图像联系起来,并利用函数的性质找出零点.
的图像联系起来,并利用函数的性质找出零点.
题型3:由函数的零点特征确定参数的取值范围
[例3] (2007·广东)已知a是实数,函数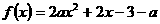 ,如果函数
,如果函数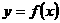 在区间
在区间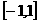 上有零点,求a的取值范围。
上有零点,求a的取值范围。
[解题思路]要求参数a的取值范围,就要从函数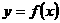 在区间
在区间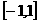 上有零点寻找关于参数a的不等式(组),但由于涉及到a作为
上有零点寻找关于参数a的不等式(组),但由于涉及到a作为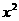 的系数,故要对a进行讨论
的系数,故要对a进行讨论
[解析] 若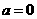 ,
, 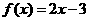 ,显然在
,显然在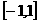 上没有零点, 所以
上没有零点, 所以 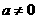 .
.
令
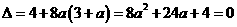 , 解得
, 解得
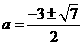
①当
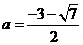 时,
时, 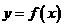 恰有一个零点在
恰有一个零点在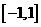 上;
上;
②当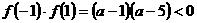 ,即
,即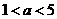 时,
时,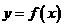 在
在
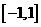 上也恰有一个零点.
上也恰有一个零点.
③当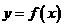 在
在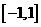 上有两个零点时, 则
上有两个零点时, 则
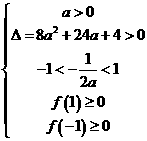 或
或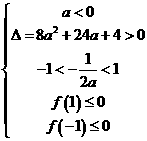
解得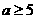 或
或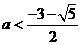
综上所求实数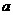 的取值范围是
的取值范围是 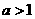 或
或 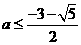 .
.
[名师指引]①二次函数、一元二次方程和一元二次不等式是一个有机的整体,也是高考热点,要深刻理解它们相互之间的关系,能用函数思想来研究方程和不等式,便是抓住了关键.
②二次函数f(x)=ax2+bx+c的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.
[新题导练]
2.给定精度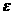 ,用二分法求函数
,用二分法求函数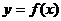 的零点近似值的步骤如下:
的零点近似值的步骤如下:
(1)确定区间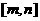 ,验证
,验证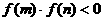 ,给定精度
,给定精度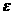 ;
;
(2)求区间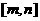 的中点
的中点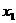 ;
;
(3)计算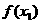 :①若
:①若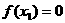 ,则
,则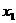 就是函数
就是函数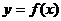 的零点;②若
的零点;②若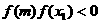 ,则令
,则令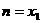 (此时零点
(此时零点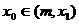 );③若
);③若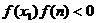 ,则令
,则令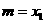 (此时零点
(此时零点
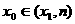 )
)
(4)判断是否达到精度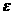 ;
;
即若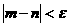 ,则得到零点值
,则得到零点值 (或
(或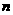 );否则重复步骤(2)-(4)
);否则重复步骤(2)-(4)
★重、难点突破
重点:函数零点的概念,掌握用二分法求函数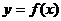 零点的近似值
零点的近似值
难点:用二分法求函数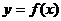 的零点近似值
的零点近似值
重难点:1.函数零点的理解
函数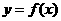 的零点、方程
的零点、方程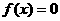 的根、函数
的根、函数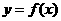 的图像与x轴交点的横坐标,实质是同一个问题的三种不同表达形式,方程
的图像与x轴交点的横坐标,实质是同一个问题的三种不同表达形式,方程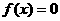 根的个数就是函数
根的个数就是函数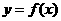 的零点的个数,亦即函数
的零点的个数,亦即函数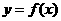 的图像与x轴交点的个数
的图像与x轴交点的个数
变号零点与不变号零点
①若函数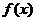 在零点
在零点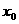 左右两侧的函数值异号,则称该零点为函数
左右两侧的函数值异号,则称该零点为函数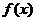 的变号零点
的变号零点
②若函数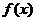 在零点
在零点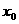 左右两侧的函数值同号,则称该零点为函数
左右两侧的函数值同号,则称该零点为函数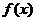 的不变号零点
的不变号零点
③若函数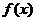 在区间
在区间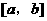 上的图象是一条连续的曲线,则
上的图象是一条连续的曲线,则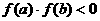 是
是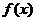 在区间
在区间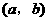 内有零点的充分不必要条件。
内有零点的充分不必要条件。
用二分法求曲线交点的坐标要注意两个问题
(1)曲线交点坐标即为方程组的解,从而转化为求方程的根
(2)求曲线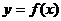 和
和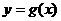 的交点的横坐标,实际上就是求函数
的交点的横坐标,实际上就是求函数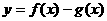 的零点,即求方程
的零点,即求方程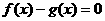 的根
的根
1.如果函数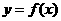 在区间
在区间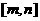 上的图像是连续不断的一条曲线,且
上的图像是连续不断的一条曲线,且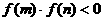 ,通过不断地把函数
,通过不断地把函数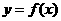 的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。
的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。
方程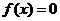 的实数根又叫做函数
的实数根又叫做函数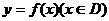 的零点。
的零点。
方程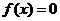 有实根
有实根 函数
函数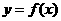 的图像与x轴有交点
的图像与x轴有交点 函数
函数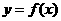 有零点;
有零点;
②如果函数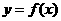 在区间
在区间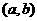 上的图像是连续不断的,且有
上的图像是连续不断的,且有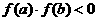 ,则函数
,则函数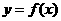 在区间
在区间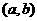 上有零点。
上有零点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com