
题目列表(包括答案和解析)
6.(四会中学09年月考)若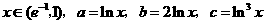 ,则( )
,则( )
A.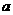 <
<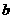 <
<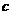 ;B.
;B.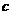 <
<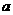 <
<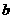 ;C.
;C.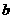 <
<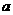 <
<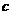 ;D.
;D.
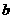 <
<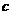 <
<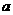
[解析] C;由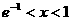 得
得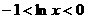 ,从而
,从而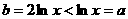 ,
,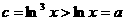
[备选例题] (广东实验中学09届月考)若函数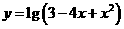 的定义域为M。当
的定义域为M。当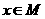 时,求
时,求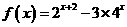 的最值及相应的x的值。
的最值及相应的x的值。
[解析]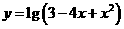 ,
,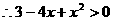 ,
,
解得: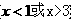 ,∴
,∴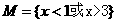
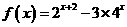 =
=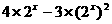
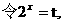 ∵
∵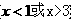 ,∴
,∴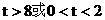
∴f(x)=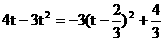 (
(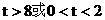 )
)
由二次函数性质可知:
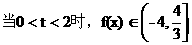 ;
;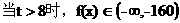
当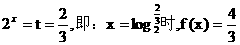
综上可知:当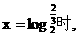 f(x)取到最大值为
f(x)取到最大值为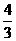 ,无最小值。
,无最小值。
★抢分频道
基础巩固训练:
5.(执信中学09届月考)已知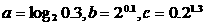 ,则
,则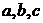 的大小关系是( )
的大小关系是( )
A.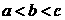 B.
B.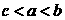 C.
C.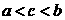 D.
D.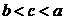
[解析] C;由于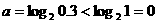 ,
,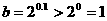 ,
,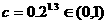 ,所以应选择C
,所以应选择C
5.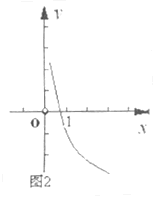 (09年山东济宁)设
(09年山东济宁)设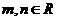 ,函数
,函数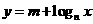 的图象如图2,则有
的图象如图2,则有
A.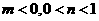 ;B.
;B.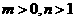
C.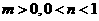 ;D.
;D.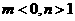
[解析] A;由图知,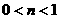 ,并且由图象知
,并且由图象知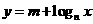
的图象是由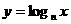 的图象向下平移得到的,故
的图象向下平移得到的,故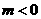
考点3 指数、对数函数的综合应用
题型1:利用对数函数的复合函数的单调性求值域
[例4] 已知x满足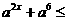
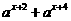
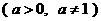 , 函数y=
, 函数y=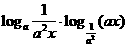 的值域为
的值域为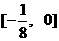 , 求a的值
, 求a的值
[解题思路]欲求a的值就设法寻找a的等式,但是这里没有等式,我们应该利用函数的单调性,求出其值域,依据已知条件寻求关于a的不等式组
[解析] 由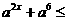
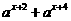
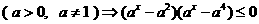
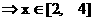
由y=
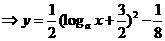 ,
,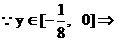
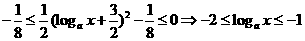 ,
, 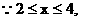
① 当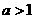 时, 为
时, 为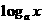 单调增函数,
单调增函数, 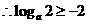 且
且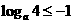 ,此时a的值不存在.
,此时a的值不存在.
② 当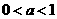 时, 为
时, 为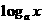 单调减函数,
单调减函数,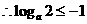 ,
,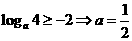 .
.
[名师指引]对数函数是重要的基本初等函数, 高考中既考查双基, 又考查对蕴含其中的函数思想、等价转化、分类讨论等思想方法的理解与运用. 因此应做到能熟练掌握它的图像与性质并能进行一定的综合运用.
题型2:指数函数与对数函数的反函数关系
[例5]设函数f(x)是函数g(x)=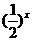 的反函数,则f(4-x2)的单调递增区间为( )
的反函数,则f(4-x2)的单调递增区间为( )
A.[0,+∞);B.(-∞,0];C.[0,2);D.(-2,0]
[解题思路] 先根据对数函数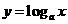 与指数函数
与指数函数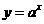 互为反函数写出函数f(x)的表达式,然后再研究复合函数的单调性求其单调递增区间
互为反函数写出函数f(x)的表达式,然后再研究复合函数的单调性求其单调递增区间
[解析]显然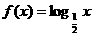 ,从而得
,从而得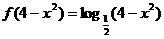 ,其定义域为
,其定义域为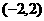
.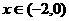 时,
时,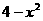 单调递增;
单调递增;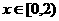 时,
时,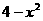 单调递减.故选C
单调递减.故选C
[名师指引] 对数函数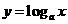 与指数函数
与指数函数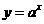 是一对特殊的基本初等函数,它们互为反函数,它们的图像关于直线y=x对称,高考中时有涉及
是一对特殊的基本初等函数,它们互为反函数,它们的图像关于直线y=x对称,高考中时有涉及
[新题导练]
∴x∈(1-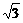 ,1]时,3-(x-1)2单调递增,从而f(x)单调递减;
,1]时,3-(x-1)2单调递增,从而f(x)单调递减;
x∈[1,1+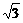 )时,3-(x-1)2单调递减,f(x)单调递增.
)时,3-(x-1)2单调递减,f(x)单调递增.
[名师指引]对数函数与二次函数的复合函数的最值(值域)与单调性是常考知识点,解决的办法就是充分利用组成复合函数的各个基本函数的单调性以及复合函数的单调性法则。
[新题导练]
4.(东皖高级中学09届月考)若函数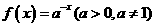 是定义域为R的增函数,
是定义域为R的增函数,
则函数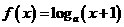 的图象大致是 ( )
的图象大致是 ( )
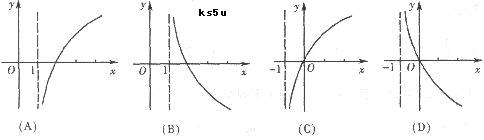
[解析] D;由函数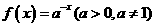 是定义域为R的增函数知
是定义域为R的增函数知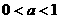 ,所以函数
,所以函数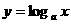 在
在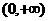 上的减函数,将
上的减函数,将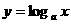 的图象向左平移一个单位即得
的图象向左平移一个单位即得
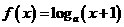 的图象,故应选D
的图象,故应选D
3.(广东吴川市09届月考)如果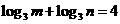 ,那么
,那么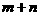 的最小值是( )
的最小值是( )
A.4;B.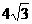 ;C.9;D.18
;C.9;D.18
[解析]18;由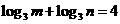 得
得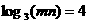 ,所以
,所以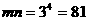 ,又由题知
,又由题知
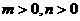 从而,
从而,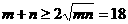 ,当且仅当
,当且仅当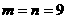 时取“=”
时取“=”
考点2对数函数的图像及性质
题型1:由函数图象确定参数的值
[例2] 函数y=log2|ax-1|(a≠0)的图象的对称轴方程是x=-2,那么a等于( )
A.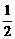 ;B.-
;B.-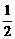 ;C.2; D.-2
;C.2; D.-2
[解题思路]由于函数图象的对称轴方程是x=-2,所以可以利用特殊值法求解
[解析] 如利用f(0)=f(-4),可得0=log2|-4a-1|.∴|4a+1|=1.
∴4a+1=1或4a+1=-1.∵a≠0,∴a=-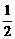 .
.
故选B
[名师指引]函数图象的对称性是常考知识点,高考要求要掌握几种基本的对称。
题型2:求复合函数值域及单调区间
[例3] 已知f(x)=log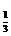 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.
[解题思路]通过研究函数f(x)的单调性
[解析] ∵真数3-(x-1)2≤3,∴log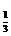 [3-(x-1)2]≥log
[3-(x-1)2]≥log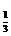 3=-1,
3=-1,
即f(x)的值域是[-1,+∞).
2.(中山市09届月考)若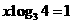 ,求
,求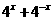 的值.
的值.
[解析] 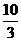 ;
;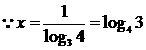 ∴
∴ 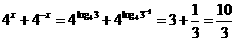
1.(高州中学09届月考)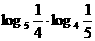 的结果是
的结果是
[解析]1;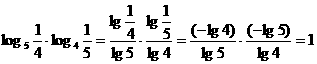
对数函数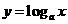 与指数函数
与指数函数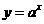 互为反函数,它们的图像关于直线y=x对称.。
互为反函数,它们的图像关于直线y=x对称.。
★重、难点突破
重点:掌握对数的运算性质及对数函数的图像与性质。
难点:综合运用对数函数的图像与性质解决问题。
重难点:1.对数函数性质的拓展
(Ⅰ)同底数的两个对数值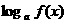 与
与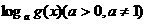 的大小比较
的大小比较
若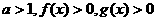 ,则
,则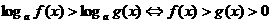
 若
若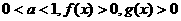 ,则
,则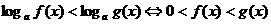
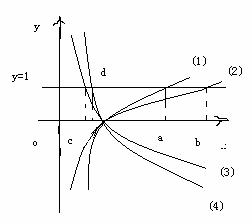
(Ⅱ)同真数的对数值大小关系如图
对应关系为
(1)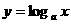 ,(2)
,(2)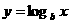 ,
,
(3)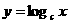 ,(4)
,(4)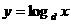
则作直线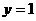 得
得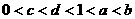
即图象在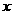 轴上方的部分自左向右底数逐渐增大
轴上方的部分自左向右底数逐渐增大
2.常见对数方程或对数不等式的解法
(1)形如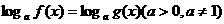 转为
转为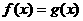 ,但要注意验根
,但要注意验根
对于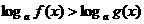 ,则
,则
当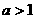 时,得
时,得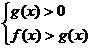 ;当
;当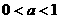 时,得
时,得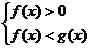
(2)形如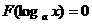 或
或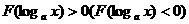 的方程或不等式,一般用换元法求解。
的方程或不等式,一般用换元法求解。
(3)形如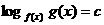 的方程化为
的方程化为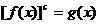 求解,对于
求解,对于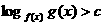 的形式可以考虑利用对数函数的单调性来解决
的形式可以考虑利用对数函数的单调性来解决
★热点考点题型探析
考点1 对数式的运算
[例1](湛江市09届高三统考)已知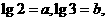 用
用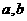 表示
表示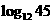
[解题思路]应设法对数换底公式将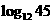 换成以常用对数,并且设法将12与45转化为2、3来表示
换成以常用对数,并且设法将12与45转化为2、3来表示
[解析]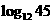
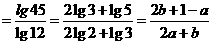
[名师指引] 对数式的运算一般都是运用对数的运算性质及对数换底公式,在未来的高考中,对数式的运算可能要综合其他知识交汇命题
[新题导练]
①函数y=logax(a>0,a≠1)叫做对数函数,其中x是自变量,图像如下
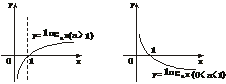
②对数函数的性质:定义域:(0,+∞); 值域:R; 过点(1,0),即当x=1时,y=0.
当a>1时,在(0,+∞)上是增函数;当0<a<1时,在(0,+∞)上是减函数。
loga(MN)=logaM+logaN. loga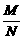 =logaM-logaN.
=logaM-logaN.
logaMn=nlogaM.(M>0,N>0,a>0,a≠1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com