5．在菱形ABCD中，若∠ABD=72°，则∠ADC=_______，∠BAD=_______．

4．若菱形的周长为16cm，则此菱形的边长是______cm．

3．菱形既是_________图形，又是_________图形，它的______都是它的对称轴．

2．菱形是特殊的_________，所以它不但具有一般_________的性质，而且还具有特殊的性质：(1)__________；(2)__________．

1．我们把__________叫做菱形．

6.2 菱形(1)同步练习

[知识盘点]

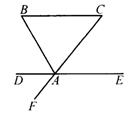
7．如图，过△ABC的顶点A作直线DE∥BC，AF是CA的延长线，图中有哪些相等的角(不计对顶角)？证明你的结论．

后花园

　　 智力操　 小明和小芳、小冲今天又在一起切磋学习数学的体会，小明给出了如下题目：

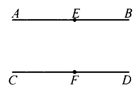
如图1，已知直线AB∥CD，点E、F分别在AB、CD上．如果在AB、CD之间有一点P，连接PE、PF，你认为∠AEP与∠CFP及∠P之间有怎样的数量关系？证明你的结论．

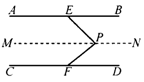
　　 小冲看完题目后，立即补完图形，很快提出猜想，并进行了证明．他的猜想是：∠AEP+∠CFP+∠EPF=360°．其证明过程如下：

　　 证明：如图2，过点P作直线MN∥AB，

　　 因为MN∥AB(已作)，

　　 所以∠AEP+∠EPM=180°(两直线平行，同旁内角互补)，

　　 因为AB∥CD(已知)，MN∥AB(已作)，

　　 所以MN∥CD(平行于同一直线的两直线互相平行)，

　　 所以∠CFP+∠FPM=180°(两直线平行，同旁内角互补)，

　　 所以∠AEP+∠CFP+∠EPF=360°．

　　 小芳看过了小冲的猜想和证明后提出质疑，认为小冲的猜想不完整．你认为小芳的质疑正确吗？说说你的理由．

6．已知：如图，AB∥CD，∠1=∠3．求证：AC∥BD．

5．如图，四边形ABCD中，AB∥CD，AD∥BC，由此你能得到哪些结论？任选你所得的1-2个结论予以证明．

拓展与延伸

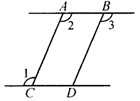
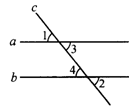
4．如图，直线a、b被直线c所截，如果∠1=∠2，能证明∠3=∠4吗？如果能，请写出你的证明过程．