1. 等边，等腰，直角；2.等边；3.B；4.5，提示：根据在直角三角形中，30°所对的直角边等于斜边的一半；5. 3；6.3，提示：过C点作垂线，转化到直角三角形和矩形解决；

10.根据等腰三角形“三线合一”的性质，等腰三角形ABC底边BC上的中线DA应垂直于底边BC(即木条)，如果重锤过点A，说明直线AD垂直于水平线，那么木条就是水平的．根据是平面内过直线外一点有且只有一条直线与已知直线垂直．

第三课时答案：

9. 证明：∵BF＝CE　 ∴BF+FC＝CE+FC，即BC＝EF

又∵AB⊥BE，DE⊥BE　 ∴∠B＝∠E＝90⁰

　又∵AC＝DF　 ∴△ABC≌△DEF,∴∠ACB＝∠DFE

　∴GF＝GC

8. (1)证明：∵AC⊥BD，∴∠ACB=∠ACD=90°．

　　 又∵AC=AC，BC=CD，∴△ACB≌△ACD(SAS)．

　　 ∴AB=AD(全等三角形的对应边相等)． ∴△ABD是等腰三角形．

(2)解：由(1)可知AB=AD， ∴∠B=∠D．又∵AC=BC， ∴∠B=∠BAC，

　　 AC=CD．∴∠D=∠DAC(等边对等角)．

　　 在△ABD中，∠B+∠D+∠BAC+∠DAC=180°，

　　 ∴2(∠BAC+∠DAC)=180°． ∴∠BAC+∠DAC=90°，

　　 即∠BAD=90°．

7. 证明：∵AD∥BC，∴∠1=∠B(两直线平行，同位角相等)，

　 ∠2=∠C(两直线平行，内错角相等)．又∵∠1=∠2，

　　 ∴∠B=∠C，

　　 ∴AB=AC(等角对等边)．

1.D；2.40°，提示：等腰三角形的顶角是100°，则底角为(180°-100°)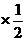=40°；3.100°，提示：根据等边对等角和三角形的外角定理得∠FEM=∠A+∠EFA=20°+80°=100°；4.C；5.4；6. .30；

8.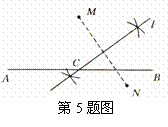 作法：(1)连接MN；

(2)作线段MN的垂直平分线，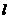

交直线AB于C点，则C点即为所求.

第二课时答案：

7.解：∵AB的垂直平分线分别交AC、AB于D、E，∴AD=BD，又∵AB+AD+BD=29 cm，AB=12 cm，∴AD=8 cm，又∵AC=12 cm，AC=AD+DC，∴DC=4 cm；

6.相等：理由：

∵AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，∴CF=CE，

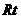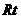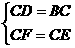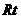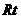在△CFD和△CEB中，，∴△CFD≌△CEB

∴BE=DF.

5. 证明：在△BDF和△CDE中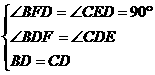

∴△BDF≌△CDE，∴DF=DE

∴D在∠A的平分线上，∴AD平分∠BAC.