
题目列表(包括答案和解析)
1. 评定学生的学科期末成绩由期考分数, 作业分数, 课堂参与分数三部分组成, 并按3:3:4的比例确定. 已知小明的数学期考80分, 作业90分, 课堂参与85分, 则他的数学期末成绩为 .
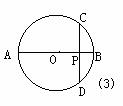
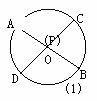
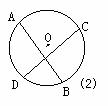
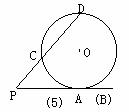
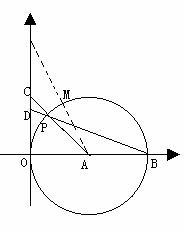
(1)经过⊙O内或⊙O外一点P作两条直线交⊙O于A、B和C、D四点(可能有重合的点),得到了如图所示的六种不同情况,在六种不同情况下,PA、PB、PC、PD四条线段之间在数量上满足的关系式可以用同一个式子表示出来,请你首先写出这个式子,然后只就图②所示的圆内两条弦相交一般情况,给出它的证明。
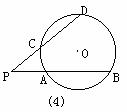
 (2)已知⊙O的半径为一定值,若点P是不在⊙O上的一个定点,请你过点P任意作一直线交⊙O于不重合的两点E、F,PE·PF的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来
(2)已知⊙O的半径为一定值,若点P是不在⊙O上的一个定点,请你过点P任意作一直线交⊙O于不重合的两点E、F,PE·PF的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来
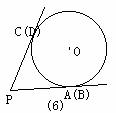
(1)如果P、Q两点同时从A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当点Q移动到BC边上(Q不于C重合)时,求作以tg∠QCA、tg∠QPA为根的一元二次方程;
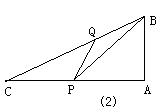
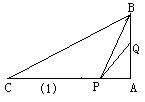 (2)如果P、Q两点同时从点A出发,以原速度按各自的移动路线到某时刻同时停止移动,当S△PBQ=
(2)如果P、Q两点同时从点A出发,以原速度按各自的移动路线到某时刻同时停止移动,当S△PBQ=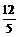 时,求PA的长。
时,求PA的长。
点P为 上任意一点(P不与O点重合),连结AP并延长交y轴于点C,连结BP并延长交y轴于点D,
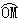 (1)当点P在 上运动时,设PC=x,
(1)当点P在 上运动时,设PC=x, 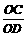 =y,
=y,
求y与x之间的函数关系式及自变量x的取值范围;
 (2)当P运动到某一位置时,恰使OB=3OD,求此时AC所在直线的解析式;
(2)当P运动到某一位置时,恰使OB=3OD,求此时AC所在直线的解析式;
(1)求b、c的取值范围;
(2)如果tg∠BAC=3,且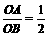 ,求b、c的值;
,求b、c的值;
(3)求出第(2)题中的抛物线上点A、B、C的坐标;
如果点P(x0,y0)在该抛物线上移动,且S△ABP>24,
求y0的取值范围。
(2)设抛物线与x轴交于A(x1,0), B(x2,0)两点(其中x2>x1>0);与y轴交于点C,
若AC·OC=BC·OA(O为原点),试求m的值,并求出这时抛物线的对称轴L。
(3)试问在抛物线y=x2-(2m+1)+m2-1的所有对称轴中,是否存在两条直线L1和L2,它们
关于(2)中所确定的直线L对称,并且与L的距离之和最大?若存在,请求出这两条对称轴L1和L2,并求出它们与L的距离之和最大值;若不存在,请说明理由。
4.现有树9棵,把它们栽成三行,要求每行恰好为4棵,试尽可能多的找出符合题意的方法。(答案略)
3.为使二次三项式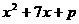 可以因式分解(在整数范围内)P可以取哪些整数?为了使式子
可以因式分解(在整数范围内)P可以取哪些整数?为了使式子
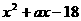 可以因工分解(在整数范围内)尽可能多地找出适合的值!(略)
可以因工分解(在整数范围内)尽可能多地找出适合的值!(略)
2.如图AB表示30米高的大楼,BC表示安装在大楼顶部的广告牌BC=6米,A.B.C在同一直线上,AD表示地面,S表示人在地面上的位置(现在还未标出)当∠BSC最大时,人看广告牌的视角最大,即观看最清晰,试确定点S,使此人观看广告牌最清晰,并求出AS的长。
(答案:可以画出经B,C且与AD相切的圆弧,切点为S,AS=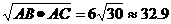 (米))
(米))
1.四边形通过一个顶点可以引一条对角线,五边形通过一个顶点可以引2条对角线,六边形通过同一个顶点可以引____条对角线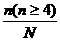 边形通过同一个顶点可以引____条对角线,试猜想
边形通过同一个顶点可以引____条对角线,试猜想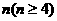 边形总共有____条对角线。(答案: 3,
边形总共有____条对角线。(答案: 3,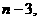
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com