
题目列表(包括答案和解析)
11、某饮料厂,经测算,用1吨水生产的钦料所获利润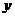 (元)是1吨水的价格
(元)是1吨水的价格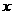 (元)的一次函数。
(元)的一次函数。
⑴ 根据下表提供的数据,求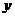 与
与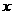 的函数关系式;当水价为每吨10元时,1吨水生产出的钦料所获利润是多少?
的函数关系式;当水价为每吨10元时,1吨水生产出的钦料所获利润是多少?
1吨水的价格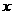 (元) (元) |
4 |
6 |
用1吨水生产的饮料所获利润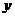 (元) (元) |
200 |
198 |
⑵ 为了节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费。已知该厂日用水量不少于20吨,设该厂日用水量为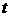 吨,当日所获利润为W元,求W与
吨,当日所获利润为W元,求W与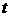 的函数关系式。该厂加强管理,积极节水,使日用水量不超过25吨。但仍不少于20吨,求该厂的日利润的取值范围。
的函数关系式。该厂加强管理,积极节水,使日用水量不超过25吨。但仍不少于20吨,求该厂的日利润的取值范围。
10、设一次函数 的图象经过第二、三、四象限,且图象与两坐标轴围成的直角三角形中有一个锐角为30°,若这个直角三角形的面积是
的图象经过第二、三、四象限,且图象与两坐标轴围成的直角三角形中有一个锐角为30°,若这个直角三角形的面积是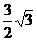 ,试求
,试求 与
与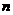 的值。
的值。
9、已知一次函数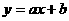 的图象经过点A(2,0 )与B(0,4)。
的图象经过点A(2,0 )与B(0,4)。
(1)求一次函数的解析式,并在直角坐标系内画出这个函数的图象;
(2)如果(1)中所求的函数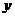 的值在-4≤
的值在-4≤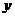 ≤4范围内,求相应的
≤4范围内,求相应的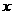 的值在什么范围内。
的值在什么范围内。
8、如图,直线PA是一次函数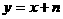 (
(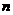 >0)的图象,直线PB是一次函数
>0)的图象,直线PB是一次函数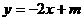 (
( >0)的图象。
>0)的图象。
(1)用 、
、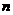 表示出点A、B、P的坐标;
表示出点A、B、P的坐标;
 (2)若点Q是PA与
(2)若点Q是PA与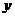 轴的交点,且四边形PQOB的面积是
轴的交点,且四边形PQOB的面积是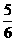 ,AB=2,试求点P的坐标,并求出直线PA与PB的解析式;
,AB=2,试求点P的坐标,并求出直线PA与PB的解析式;
7、已知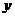 与
与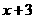 成正比例,且
成正比例,且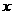 =0时,
=0时,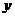 =-3。求出
=-3。求出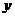 与
与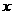 之间的函数关系式;在直角坐标系中画出这个函数的图象;根据图象回答函数值
之间的函数关系式;在直角坐标系中画出这个函数的图象;根据图象回答函数值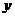 随自变量
随自变量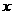 增大而怎样变化的?
增大而怎样变化的?
6、已知二次函数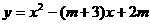
(1)证明;不论 取什么实数,该函数的图象与
取什么实数,该函数的图象与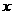 轴一定有两个交点;
轴一定有两个交点;
(2) 取什么值时,两个交点之间的距离等于3 ?
取什么值时,两个交点之间的距离等于3 ?
5、已知一条抛物线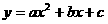 经过点(2,0)与(12,0);最高点的纵坐标是3,求这条抛物线的解析式。
经过点(2,0)与(12,0);最高点的纵坐标是3,求这条抛物线的解析式。
4、已知拖拉机油箱最多可装油54千克,装满后耕地每小时耗油6千克。求:
(1)油箱中剩油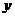 千克与时间
千克与时间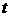 (小时)之间的函数关系及
(小时)之间的函数关系及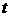 的取值范围;
的取值范围;
(2)工作4小时36分后,油箱中还剩多少油。
3、已知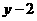 与
与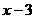 成正比例关系,且图象过(4,4)
成正比例关系,且图象过(4,4)
(1)求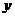 与
与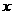 的函数关系式;
的函数关系式;
(2)写出直线与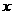 轴,
轴,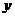 轴交点A、B的坐标;
轴交点A、B的坐标;
(3)求直线与两坐标轴围成的三角形面积S△AOB
 1、如图,四边形AOCB是直角梯形,AB//OC,OA=10,AB=9,∠OCB=45°,求点A、B、C的坐标及直角梯形AOCB的面积。
1、如图,四边形AOCB是直角梯形,AB//OC,OA=10,AB=9,∠OCB=45°,求点A、B、C的坐标及直角梯形AOCB的面积。
2、 已知一次函数
已知一次函数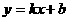 的图象如图所示。求
的图象如图所示。求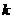 、
、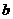 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com