
题目列表(包括答案和解析)
1、下列给出的对象中,能表示集合的是( )
A、一切很大的数 B、无限接近零的数
C、聪明的人
D、方程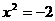 的实数根
的实数根
22.(本小题满分14分)
已知集合M是同时满足下列两个性质的函数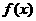 的全体:
的全体:
①函数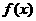 在其定义域上是单调函数;
在其定义域上是单调函数;
②在函数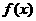 的定义域内存在闭区间
的定义域内存在闭区间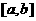 使得
使得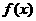 在
在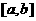 上的最小值是
上的最小值是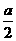 ,且最大值是
,且最大值是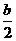 . 请解答以下问题
. 请解答以下问题
(1) 判断函数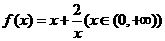 是否属于集合
是否属于集合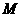 ?并说明理由;
?并说明理由;
(2)判断函数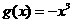 是否属于集合
是否属于集合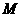 ?并说明理由.若是,请找出满足②的闭区间
?并说明理由.若是,请找出满足②的闭区间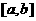 ;
;
(3)若函数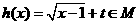 ,求实数
,求实数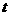 的取值范围.
的取值范围.
21.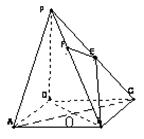 (本题满分12分)
(本题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
作EF⊥PB交PB于点F.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
20.(本题满分12分)
某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造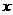 架该种飞机的产值
架该种飞机的产值
函数为 (单位:万元),成本函数
(单位:万元),成本函数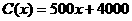 (单位:万元)。
(单位:万元)。
利润是收入与成本之差,又在经济学中,函数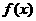 的边际利润函数
的边际利润函数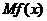 定义为:
定义为: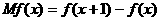
(1)、求利润函数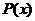 及边际利润函数
及边际利润函数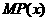 ;(利润=产值-成本)
;(利润=产值-成本)
(2)、问该公司的利润函数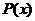 与边际利润函数
与边际利润函数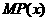 是否具有相等的最大值?
是否具有相等的最大值?
19. (本题满分12分)
(本题满分12分)
一个高为16的圆锥内接于一个体积为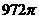 的球,在圆锥内
的球,在圆锥内
又有一个内切球;求
(1)圆锥的侧面积;
(2)圆锥的内切球的体积.
18.(本题满分12分)
(1)求经过直线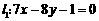 和
和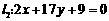 的交点,且平行于直线
的交点,且平行于直线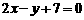 的直线方程.
的直线方程.
(2)已知直线l的方程是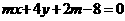 , 圆C的方程是
, 圆C的方程是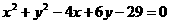
求直线l被圆截得的弦长最短时的l的方程.
17.(本题满分12分)
(1)求值: 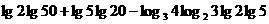
(2)已知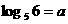 ,
,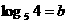 . 用
. 用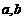 表示
表示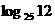 .
.
13.  14. 15. 16.
14. 15. 16.
16.下列说法:①若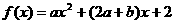 (其中
(其中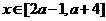 )是偶函数, 则实数
)是偶函数, 则实数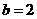 ;②
;②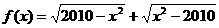 既是奇函数又是偶函数;③已知
既是奇函数又是偶函数;③已知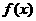 是定义在
是定义在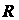 上的奇函数,若当
上的奇函数,若当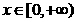 时,
时, 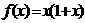 ,则当
,则当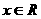 时,
时, 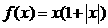 ;④已知
;④已知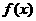 是定义在R上的不恒为零的函数, 且对任意的
是定义在R上的不恒为零的函数, 且对任意的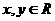 都满足
都满足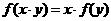
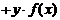 , 则
, 则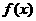 是奇函数.其中所有正确说法的序号是 __
是奇函数.其中所有正确说法的序号是 __
|

 2009-2010学年第一学期高一年级期末考试数学答题卷
2009-2010学年第一学期高一年级期末考试数学答题卷15.在三棱锥V-ABC中,当三条侧棱VA、VB、VC满足_________时,VC⊥AB(填上你认为正确的一种条件即可).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com