
题目列表(包括答案和解析)
1.直线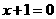 的斜率为
的斜率为
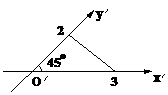 A.
0
B. -1
C.
A.
0
B. -1
C. 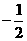 D. 不存在
D. 不存在
 得分 评卷人 20.本题满分10分(每小题各5分)
得分 评卷人 20.本题满分10分(每小题各5分)
(1)已知二次函数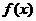 的两个零点分别是 -2和4,且其图象经过点(-1,-10),试求函数
的两个零点分别是 -2和4,且其图象经过点(-1,-10),试求函数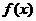 的最小值.
的最小值.
(2)计算: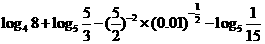 .
.
 得 分 评卷人 21.本题满分8分
得 分 评卷人 21.本题满分8分
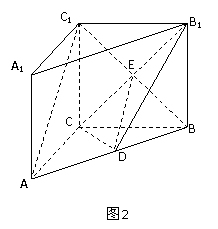 如图2:在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5,点D是AB的中点,CB1与BC1相交于点E.
如图2:在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5,点D是AB的中点,CB1与BC1相交于点E.
(1)求证:AC⊥BC1;
(2)求线段DE的长.
 得 分 评卷人 22.本题满分8分
得 分 评卷人 22.本题满分8分
已知圆C: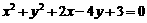 .
.
(1)若不经过坐标原点的直线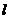 与圆C相切,且直线
与圆C相切,且直线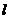 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线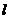 的方程;
的方程;
(2)设点P在圆C上,求点P到直线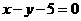 距离的最大值与最小值.
距离的最大值与最小值.
 得 分 评卷人 23.本题满分8分
得 分 评卷人 23.本题满分8分
社区文具商场的某种毛笔每支售价25元,书法练习本每本售价5元.该商场为促销制定了甲、乙两种优惠方案:方案甲:买1支毛笔就赠送1本书法练习本;方案乙:按购买金额打9折付款.某校书法兴趣小组打算购买这种毛笔10支,这种书法练习本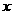 (
( )本.
)本.
(1)分别写出按甲、乙两种优惠方案实际付款金额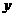 甲(元)、
甲(元)、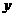 乙(元)与
乙(元)与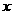 之间的函数关系式;
之间的函数关系式;
(2)如果该商场即允许只选择一种优惠方案购买,也允许同时用两种优惠方案购买,请你就购买这种毛笔10支和这种书法练习本60本设计一种最省钱的购买方案.
 得 分 评卷人 24.本题满分9分
得 分 评卷人 24.本题满分9分
已知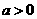 且
且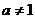 ,
,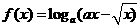 .
.
(1)求函数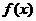 的定义域;
的定义域;
(2)当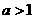 时,判断函数
时,判断函数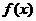 的单调性,并用函数单调性的定义证明你的结论.
的单调性,并用函数单调性的定义证明你的结论.
抚顺市普通高中2009--2010学年度第一学期期末教学质量检测
20.(本小题满分14分)已知函数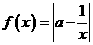 (
(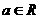 ).
).
(1) 试确定实数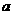 的值,使函数
的值,使函数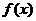 在其定义域上为偶函数;
在其定义域上为偶函数;
(2) 若函数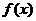 的图象过
的图象过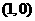 点,试探究是否存在实数
点,试探究是否存在实数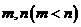 ,使得函数
,使得函数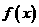 的定义域和值域都是
的定义域和值域都是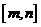 ?若存在,请求出
?若存在,请求出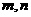 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
19.(本小题满分14分)已知二次函数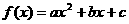 ,函数
,函数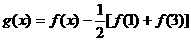 .
.
(1)若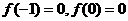 ,求出函数
,求出函数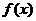 的零点;
的零点;
(2)若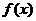 满足
满足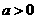 且
且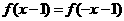 ;又
;又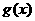 在区间
在区间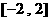 上的最大值为
上的最大值为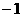 ,求
,求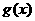 的表达式;
的表达式;
 (3)若
(3)若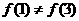 ,证明方程
,证明方程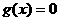 必有一个实数根属于区间
必有一个实数根属于区间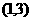 .
.
18.(本小题满分12分)为治疗某种流行疾病,医生让某患者服用一种抗生素,规定每天早上八时服一片,现知该药片每片含药量为200毫克,他的肾脏每天可从体内滤出这种药的60%,问:
⑴ 经过多少天,该患者所服的第一片药在他体内残留不超过1毫克?(lg2=0.3)
⑵ 如果抵抗这种疾病要求体内的药物含量不低于40毫克,该患者自服药起的5天内都能抵抗这种疾病,那么该患者应至少连续服药多少天?
17.(本小题满分14分)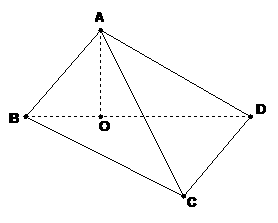 如图,在三棱锥
如图,在三棱锥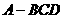 中,
中,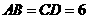 ,
,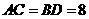 ,
,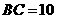 ,且
,且 在平面
在平面 上的射影
上的射影 恰好在
恰好在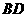 上.
上.
(1)求证: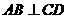 ;
;
(2)求证: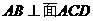 ;
;
(3)求三棱锥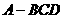 的体积.
的体积.
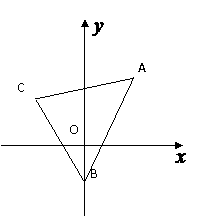
16.(本小题满分14分)如图,已知三角形的顶点为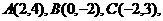 求:
求:
 (1)
(1)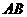 边上的中线
边上的中线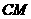 所在直线的方程;
所在直线的方程;
(2)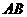 边上的高所在直线的方程;
边上的高所在直线的方程;
(3)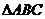 的面积.
的面积.

15.(本小题满分12分)已知全集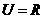 ,集合
,集合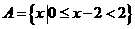 ,
,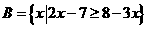 ,求:
,求:
(1)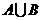 ;
;
(2)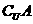 ;
;
(3)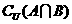 .
.
14. 如图,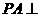 ⊙
⊙ 所在的平面,
所在的平面,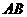 是⊙
是⊙ 的直径,
的直径,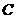 是⊙
是⊙ 上
上
的一点,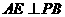 于
于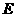 ,
,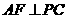 于
于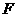 ,给出下列结论:
,给出下列结论:
①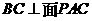 ;②
;②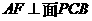 ;③
;③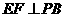 ;④
;④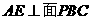 .
.
其中正确命题是 .
13.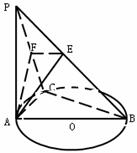 若函数
若函数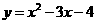 的定义域是
的定义域是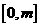 ,值域为
,值域为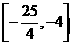 ,则满足条件的实数
,则满足条件的实数 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com