
题目列表(包括答案和解析)
13过P(1,2)且与原点距离最远的直线方程为___________.
14已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=1,则球面面积为___________-.
15在xOy平面上,四边形ABCD的四个顶点坐标依次为(0,0)、(1,0)、(2,1)、(0,3),则这个四边形绕x轴旋转一周所得到的几何体的体积为__________.
16如图3,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是___________.
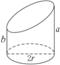
图3
1下列命题正确的是( )
A.因为直线向两方无限延伸,所以直线不可能在平面内
B.如果线段的中点在平面内,那么线段在平面内
C.如果线段上有一个点不在平面内,那么线段就不在平面内
D.当平面经过直线时,直线上可以有不在平面内的点
2过点(-1,1)和(3,9)的直线在x轴上的截距为( )
A.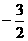 B.
B.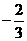 C.
C.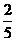 D.2
D.2
3在正方体ABCD-A1B1C1D1中,与AD成异面直线的棱共有( )
A.4条 B.5条 C.6条 D.7条
4点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围是( )
A.-1<a<1 B.0<a<1
C.a<-1或a>1 D.a=±1
5球的面积膨胀为原来的3倍,膨胀后的球的体积为原来的( )
A.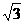 倍
B.
倍
B.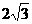 倍
C.
倍
C.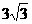 倍 D.4倍
倍 D.4倍
6下列命题:
①一条直线在平面内的射影是一条直线.
②在平面内射影是直线的图形一定是直线.
③在同一平面内的射影长相等,则斜线长相等.
④两斜线与平面所成的角相等,则这两斜线互相平行.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
7已知空间两个动点A(m,1+m,2+m)、B(1-m,3-2m,3m),则AB的最小值是( )
A.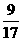 B.
B.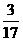 C.
C.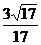 D.
D.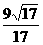
8正方形ABCD沿对角线BD折成直二面角后,下列结论不成立的是( )
A.AC⊥BD
B.△ADC为正三角形
C.AB、CD所成角为60°
D.AB与面BCD所成角为60°
9从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为( )
()
A.π B.2π C.4π D.6π
10a、b∈N*,则同时过不同三点(a,0)、(0,b)、(1,3)的直线条数为( )
A.1 B.2 C.3 D.多于3
 11图2,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=
11图2,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=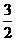 ,EF与面AC的距离为2,则该多面体的体积为…( ) ()
,EF与面AC的距离为2,则该多面体的体积为…( ) ()
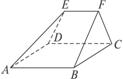
图2
A.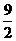 B.5
C.6
D.
B.5
C.6
D.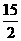
12光线从点A(-1,1)射出经x轴反射到圆C:(x-5)2+(y-7)2=4的最短路程是( )
A. -2 B.8 C.
-2 B.8 C.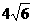 D.10
D.10
22.(本小题满分12分)已知函数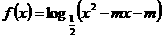 .
.
(1)若 =1,求函数
=1,求函数 的定义域;k+s-5#u
的定义域;k+s-5#u 
(2)若函数 的值域为R,求实数
的值域为R,求实数 的取值范围;
的取值范围;
|
 在区间
在区间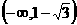 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.21.(本小题满分12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4米(高不变);二是高度增加4米(底面直径不变)。
(1) 分别计算按这两种方案所建的仓库的体积;
(2) 分别计算按这两种方案所建的仓库的表面积;
(3)
哪个方案更经济些?k+s-5#u

20.(本小题满分12分)
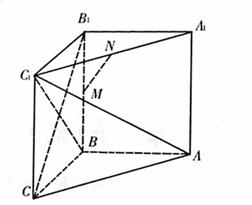 如图所示,在三棱柱ABC-A1B1C1中,∠ABC=90°,三条侧棱都与底面垂直,M、N分别为BB1、A1C1的中点.
如图所示,在三棱柱ABC-A1B1C1中,∠ABC=90°,三条侧棱都与底面垂直,M、N分别为BB1、A1C1的中点.
(1)求证:AB⊥CB1;k+s-5#u 
(2)求证:MN//平面ABC1.
19.(本小题满分12分)已知函数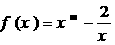 且
且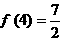
(1).求m的值k+s-5#u 
(2)判断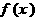 的奇偶性
的奇偶性
18.(本小题满分12分)
已知直线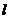 经过点P(-2,5),且斜率为
经过点P(-2,5),且斜率为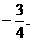 k+s-5#u
k+s-5#u 
(1)求直线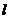 的方程;
的方程;
(2)若直线m与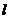 平行,且点P到直线m的距离为3,求直线m的方程.
平行,且点P到直线m的距离为3,求直线m的方程.
17.(本小题满分10分)已知M={1,2,a2-3a-1 },N={-1,a,3},M∩N={3},求实数a的值.
16.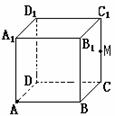 如右图.M是棱长为2cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.k+s-5#u
如右图.M是棱长为2cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.k+s-5#u 
15.已知函数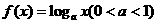 ,对于下列命题:
,对于下列命题:
①若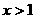 ,则
,则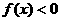 ; ②若
; ②若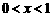 ,则
,则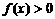 ; k+s-5#u
; k+s-5#u

③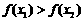 ,则
,则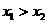 ; ④
; ④ .
.
其中正确的命题的序号是 (写出所有正确命题的序号).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com