
题目列表(包括答案和解析)
1.(本小题12分)已知函数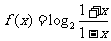 ,
,
1)求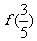 和
和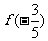 ;
;
2)判断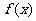 的奇偶性,并说明理由。
的奇偶性,并说明理由。
12.(本小题满分14分)
解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为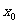 个,则
个,则
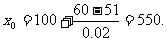
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元.
(2)当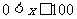 时,P=60;
时,P=60;
当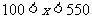 时,
时,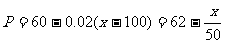 ;
;
当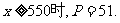
所以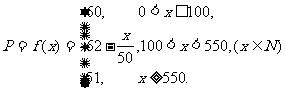
(3)设销售商的一次订购量为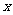 个时,工厂获得的利润为y元,则
个时,工厂获得的利润为y元,则
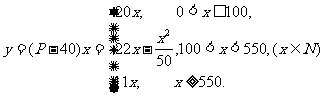
当x=500时,y=6000;当x=1000时,y=11000.
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,利润是11000元.
11.(本小题满分14分)
解:四边形ABCD绕AD旋转一周所成的
几何体,如右图:
 S表面=S圆台下底面+S圆台侧面+
S圆锥侧面 V
=V圆台-V圆锥
S表面=S圆台下底面+S圆台侧面+
S圆锥侧面 V
=V圆台-V圆锥
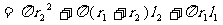
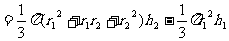
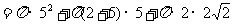
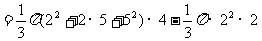
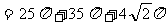
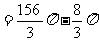
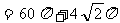
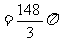
10.(本小题满分14分)
解:(1)证明:在(-∞,+∞)上任取两个值x1,x2且x1<x2
f(x1)-f(x2)= (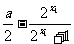 )-(
)-(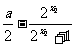 )
)
=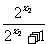 -
-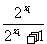 =
=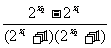
∵2>1且x1<x2 ∴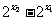 >0又
>0又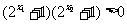
∴f(x1)-f(x2)>0即f(x1)>f(x2) ∴函数f(x)在(-∞,+∞)上是减函数。
(2)∵f(x)为奇函数且在x=0处有意义,∴f(0)=0
 ∴
∴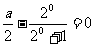 ∴
∴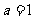
9.(本小题满分12分)
解:由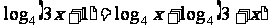 得
得
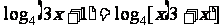

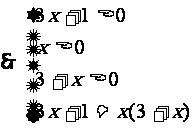
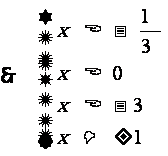
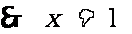
8.(本小题满分14分)
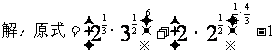 解:原式=
解:原式=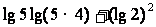
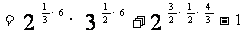
 =
=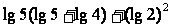
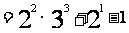 =
=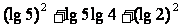
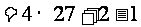 =
=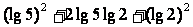
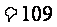 =
=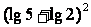
=1
7.(本小题满分12分)
解:由函数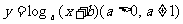 得
得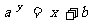
把两点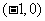 和
和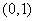 代入上式可得:
代入上式可得:
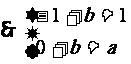
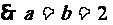
5、解:(A)(1)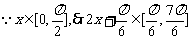
则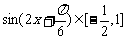 ,
,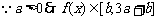 ,则
,则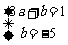 ,
,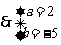
(2) 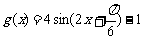 ,
,
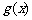 的单调递增区间为
的单调递增区间为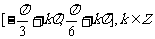
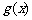 的单调递减区间为
的单调递减区间为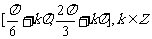
(B)(1)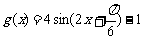
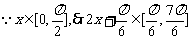
则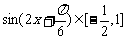 ,当a=0不合题意
,当a=0不合题意
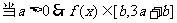 ,则
,则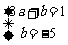 ,
,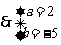
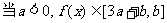 则
则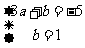 ,
,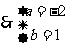
(2)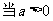 ,即a=2,b=-5时
,即a=2,b=-5时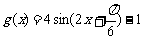 ,且
,且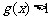 即
即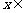
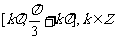
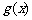 的单调递增区间为
的单调递增区间为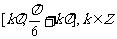
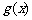 的单调递减区间为
的单调递减区间为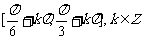
6解:(1)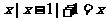 所以
所以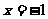 或
或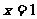 ;
;
(2)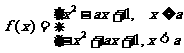 ,
,
1O.当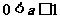 时,
时,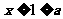 ,这时,
,这时,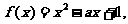 对称轴
对称轴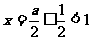 ,
,
所以函数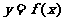 在区间
在区间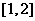 上递增,
上递增,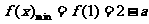 ;
;
2O.当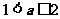 时,
时,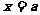 时函数
时函数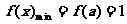 ;
;
3O.当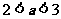 时,
时,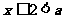 ,这时,
,这时,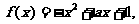 对称轴
对称轴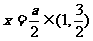 ,
,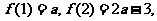
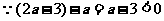 所以函数
所以函数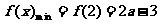 ;
;
(3)因为 所以
所以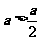 ,所以
,所以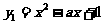 在
在 上递增;
上递增;
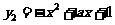 在
在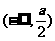 递增,在
递增,在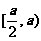 上递减.
上递减.
因为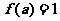 ,所以当
,所以当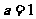 时,函数
时,函数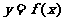 的图像与直线
的图像与直线 有2个交点;
有2个交点;
又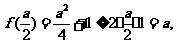 当且仅当
当且仅当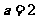 时,等号成立.
时,等号成立.
所以,当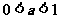 时,函数
时,函数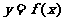 的图像与直线
的图像与直线 有1个交点;
有1个交点;
当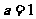 时,函数
时,函数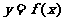 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当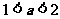 时,函数
时,函数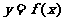 的图像与直线
的图像与直线 有3个交点;
有3个交点;
当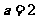 时,函数
时,函数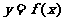 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当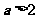 时,函数
时,函数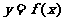 的图像与直线
的图像与直线 有3个交点.
有3个交点.
11.8-p>0及p>0得定义域为0<p<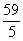 .
.
(2)由y≥14,得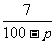 (118-10p)p≥14.
(118-10p)p≥14.
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤10.
故当比率在[2%,10%]内时,商场收取的管理费将不少于14万元.
(3)第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)=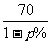 (11.8-p)(2≤p≤10).
(11.8-p)(2≤p≤10).
∵g(p)=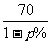 (11.8-p)=700(10+
(11.8-p)=700(10+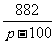 )为减函数,
)为减函数,
∴g(p)max=g(2)=700(万元).
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元
4. 解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为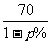 (11.8-p)万元,
(11.8-p)万元,
则商场该年对该商品征收的总管理费为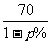 (11.8-p)p%(万元).
(11.8-p)p%(万元).
故所求函数为:y=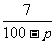 (118-10p)p.
(118-10p)p.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com