
题目列表(包括答案和解析)
9.(本小题满分12分)
某租车公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加60元时,未租出的车将会增加一辆。租出的车每月需要维护费160元,未租出的车每月需要维护费60元。 (Ⅰ)当每辆车的月租金定为3900元时,能租出多少辆车? (Ⅱ)当每辆车的月租金为多少元时,租车公司的月收益最大?最大月收益是多少?
8.(本小题满分12分)
已知二次函数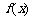 满足
满足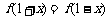 ,且
,且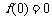 ,
,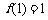 ,若
,若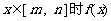 的值域也为 [ m,n ],求m,n.
的值域也为 [ m,n ],求m,n.
7.(本小题满分12分)
已知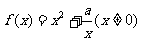 ,讨论
,讨论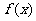 的奇偶性,并说明理由。
的奇偶性,并说明理由。
6.(本小题满分10分)
若集合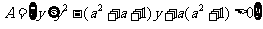 ,
,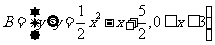
(1)若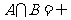 ,求实数a的取值范围
,求实数a的取值范围
(2)当a取使不等式 恒成立的最小值时,求
恒成立的最小值时,求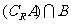
5.
已知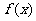 是定义在R上的函数,
是定义在R上的函数,
设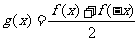 ,
,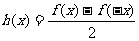
1 试判断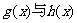 的奇偶性;
的奇偶性;
2 试判断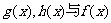 的关系;
的关系;
3 由此你能猜想得出什么样的结论,并说明理由.
4.已知集合A={a,a+b,a+2b},B={a,ac,ac2}.若A=B,求实数c的值.



3.集合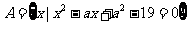
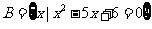 ,
,

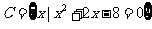 满足
满足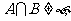 ,
,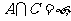 求实数
求实数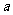 的值。
的值。
2.已知f(x)为偶函数且f(x)在(0,+∞)上为增函数,则f(x)在(-∞,0)上是增函数还是减函数?判断并给予证明

1.设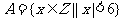 ,
,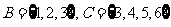 ,
,
 求:(1)
求:(1)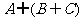 ;(2)
;(2)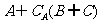
11.(本小题满分10分)
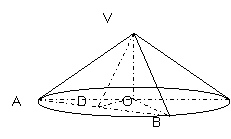 解:(1)由已知得,圆锥底面半径r=
解:(1)由已知得,圆锥底面半径r=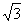 ,h=1,如图,
,h=1,如图,
设过圆锥顶点的截面为VAB,过底面圆心O
作OD⊥AB于D,并设OD=x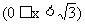 ,
,
则VD=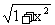 ,DA=
,DA=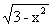 ,所以截面VAB的面积
,所以截面VAB的面积
S=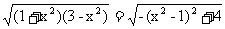 ,故当x=1时,S最大为2 ……………5 分
,故当x=1时,S最大为2 ……………5 分
(2)由(1)得,OD⊥AB,VD⊥AB,所以,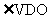 就是二面角V-AB-O的平面角,即截面与底面所成锐二面角的平面角,由(1)知在Rt△VDO中,VO=OD=1,所以
就是二面角V-AB-O的平面角,即截面与底面所成锐二面角的平面角,由(1)知在Rt△VDO中,VO=OD=1,所以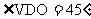 ……10分
……10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com