
题目列表(包括答案和解析)
6.(本题共10分)
(1)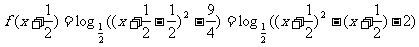
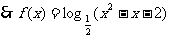
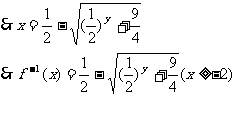
(2)由
又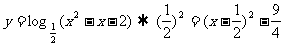
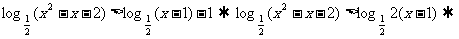
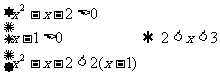
5. 解:(1)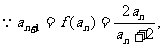
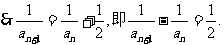 所以
所以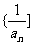 成等差数列
成等差数列
所以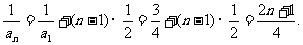
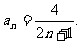 …
…
(2)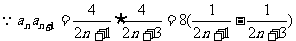
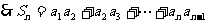
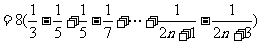
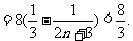 …………14分
…………14分
4. n=1时,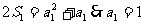
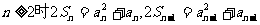
相减得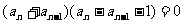
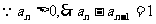 ∴数列{an}是等差数列,公差为1∴an=n
∴数列{an}是等差数列,公差为1∴an=n
(2)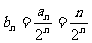
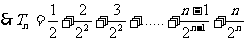

3. 解;由S4≠2S2知q≠1
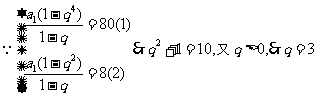
将q=3代入(1)中得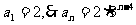
设数列{bn}公差为d,则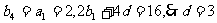
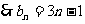
2.解(I)依题意M(2,2),A(4,5),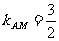 ,设直线AC的斜率为
,设直线AC的斜率为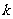 ,则
,则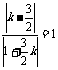 ,解得
,解得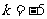 或
或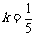 ,故所求直线AC的方程为
,故所求直线AC的方程为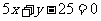 或
或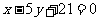 .
.
(II)圆的方程可化为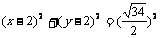 ,设A点的横坐标为
,设A点的横坐标为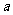 。
。
则纵坐标为 .
.
1当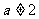 时,
时,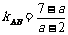 ,设AC的斜率为
,设AC的斜率为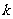 ,把∠BAC看作AB到AC的角,则可得
,把∠BAC看作AB到AC的角,则可得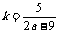 ,直线AC的方程为
,直线AC的方程为
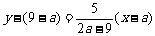 ,
,
即 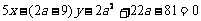 ,
,
又点C在圆M上,所以只需圆心到AC的距离小于等于圆的半径,
即 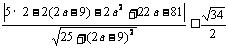 ,化简得
,化简得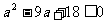 ,解得
,解得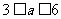 ;
;
2当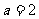 时,则A(2,7)与直线
x=2成45°角的直线为
时,则A(2,7)与直线
x=2成45°角的直线为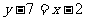 即
即 M到它的距离
M到它的距离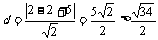 ,这样点C不在圆M上,还有
,这样点C不在圆M上,还有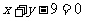 显然也不满足条件,故A点的横坐标范围为[3,6].
显然也不满足条件,故A点的横坐标范围为[3,6].
1. 由
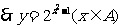 的值域为(1,8)
的值域为(1,8)
10.(本小题满分12分)已知圆C: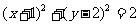
(1)若圆C的切线在x轴和y轴的截距相等,求此切线的方程
(2)从圆外一点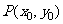 向该圆引一条切线, 切点为M,O为坐标原点,
向该圆引一条切线, 切点为M,O为坐标原点,
且有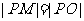 , 求使得
, 求使得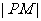 取最小值时点P的坐标高§考§资§源§网
取最小值时点P的坐标高§考§资§源§网
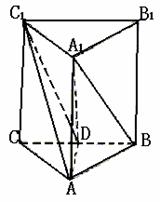 11.如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AB=a.
11.如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AB=a.
 (Ⅰ)求证:直线A1D⊥B1C1;
(Ⅰ)求证:直线A1D⊥B1C1;
 (Ⅱ)求点D到平面ACC1的距离;
(Ⅱ)求点D到平面ACC1的距离;
 (Ⅲ)判断A1B与平面ADC的位置关系,并证明你的结论.(12分)
(Ⅲ)判断A1B与平面ADC的位置关系,并证明你的结论.(12分)
9.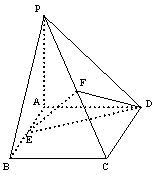 (本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(1)求证:CD⊥PD;
(2)求证:EF∥平面PAD;
(3)当平面PCD与平面ABCD成多大角时,
直线EF⊥平面PCD?
8.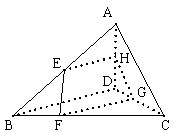 (本小题满分11分)已知: 空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且
(本小题满分11分)已知: 空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且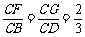 .
.
求证:(1)E、F、G、H四点共面;
(2)三条直线EF、GH、AC交于一点.
7. (本小题满分10分) 已知: 在△ABC中,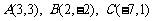 .
.
求: (1) AB边上的高CH所在直线的方程.
(2) AB边上的中线CM所在直线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com