
题目列表(包括答案和解析)
5.(A)已知 ,函数
,函数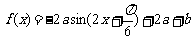 ,当
,当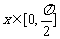 时,
时,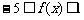 .(1)求常数
.(1)求常数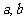 的值
的值
(2)设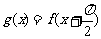 ,求
,求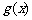 的单调区间
的单调区间
(B)已知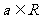 ,函数
,函数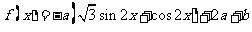 ,当
,当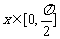 时,
时,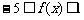 .
.
(1)求常数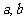 的值
的值
(2)当a>0时,设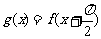 ,且
,且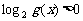 ,求
,求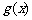 的单调区间
的单调区间
4.某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件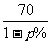 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函
数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征
收管理费的比率p%的范围是多少?
(3)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金
额,则p应为多少?
3.已知函数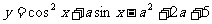 有最大值
有最大值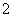 ,试求实数
,试求实数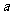 的值
的值
2.已知关于x的方程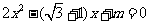 的两根为
的两根为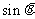 和
和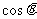 ,
,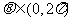 ,求:(1)
,求:(1)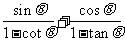 的值;
的值;
(2) 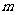 的值;
的值;
(3) 方程的两根及此时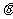 的值.
的值.
1.已知角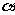 的顶点与直角坐标系的原点重合,始边在x轴的正半轴上,
的顶点与直角坐标系的原点重合,始边在x轴的正半轴上,
终边经过点P(-1,2),
求(1)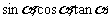
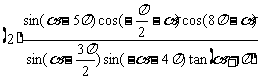
11.解(Ⅰ)证法一:∵点D是正△ABC中BC边的中点,∴AD⊥BC,
又A1A⊥底面ABC,∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.
证法二:连结A1C1,则A1C=A1B. ∵点D是正△A1CB的底边中BC的中点,
∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.
(Ⅱ)解法一:作DE⊥AC于E, ∵平面ACC1⊥平面ABC,
∴DE⊥平面ACC1于E,即DE的长为点D到平面ACC1的 距离. 在Rt△ADC中,
AC=2CD=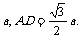
∴所求的距离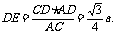
解法二:设点D到平面ACC1的距离为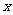 ,
,
∵体积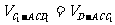
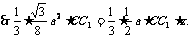
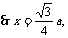 即点D到平面ACC1的距离为
即点D到平面ACC1的距离为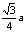 .
.
(Ⅲ)答:直线A1B//平面ADC1,证明如下:
证法一:如图1,连结A1C交AC1于F,则F为A1C的中点,∵D是BC的中点,∴DF∥A1B,
又DF 平面ADC1,A1B
平面ADC1,A1B 平面ADC1,∴A1B∥平面ADC1.
平面ADC1,∴A1B∥平面ADC1.
证法二:如图2,取C1B1的中点D1,则AD∥A1D1,C1D∥D1B,
∴AD∥平面A1D1B,且C1D∥平面A1D1B,
∴平面ADC1∥平面A1D1B,∵A1B 平面A1D1B,∴A1B∥平面ADC1.
平面A1D1B,∴A1B∥平面ADC1.
10. 解:(1)当截距不为零时:设切线方程为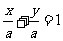 即:
即: 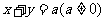
圆C为: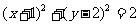 , 圆心为C(-1,2),到切线距离等于圆的半径
, 圆心为C(-1,2),到切线距离等于圆的半径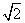
所以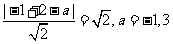 ----------------------------------------3分
----------------------------------------3分
当截距等于零时:设切线方程为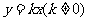 , 同理可得
, 同理可得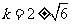 ----------5分
----------5分
所以所求切线方程为:
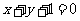 或
或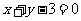 或
或 或
或 ------------------------6分
------------------------6分
(2)∵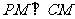 ,∴
,∴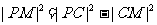 ,又
,又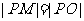
∴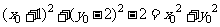 , 整理得:
, 整理得: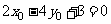 -----------------9分
-----------------9分
即动点P在直线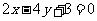 上, 所以
上, 所以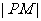 的最小值就是
的最小值就是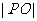 的最小值,
的最小值,
过点O作直线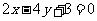 的垂线,垂足为P ,
的垂线,垂足为P ,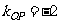
解方程组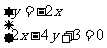 得
得 所以点P坐标为
所以点P坐标为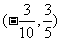 --------------12分
--------------12分
9. 解:(1)证明:∵PA⊥底面ABCD,CD 平面ABCD,∴PA⊥CD.
平面ABCD,∴PA⊥CD.
又∵ CD⊥AD,CD⊥平面PAD. ∴CD⊥PD. ------------------------4分
(2) 取PD中点M ,连结FM,AM, ∵F为PC中点∴FM∥CD, 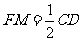
∵E为AB中点, ABCD为矩形, ∴AE∥CD, 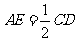 , ∴AE∥FM,AE=FM,
, ∴AE∥FM,AE=FM,
∴AEFM是平行四边形, ∴EF∥AM, ∵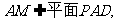 ∴
∴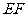 ∥
∥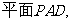 ---- 8分
---- 8分
(3)取CD中点, 连结FG, EG
∵E , G为矩形ABCD中AB , CD中点, ∴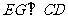 , ∵F , G为PC ,CD中点,
, ∵F , G为PC ,CD中点,
∴FG∥AD, 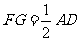 , ∵
, ∵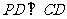 ∴
∴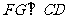
∴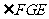 为二面角P-CD-A的平面角高§考§资§源§网
为二面角P-CD-A的平面角高§考§资§源§网
∵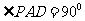 , M为AD中点, ∴
, M为AD中点, ∴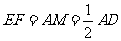 ,∴EF=FG
,∴EF=FG
又∵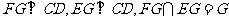 , ∴
, ∴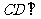 平面EFG, ∵
平面EFG, ∵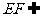 平面EFG,
平面EFG,
∴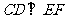 , ∵
, ∵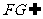 面PCD ,
面PCD , 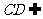 面PCD ,
面PCD , 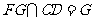 ,
,
∴当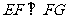 即
即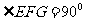 时,
时, 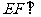 面PCD , 此时
面PCD , 此时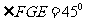 -----------------12分高§考§资§源§网
-----------------12分高§考§资§源§网
8. 证明:(1) 在△ABD和△CBD中,
∵ E、H分别是AB和CD的中点, ∴ EH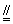
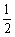 BD.又 ∵
BD.又 ∵ 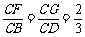 ,
,
∴ FG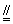
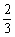 BD. ∴ EH∥FG. 所以,E、F、G、H四点共面.
-------------------------5分
BD. ∴ EH∥FG. 所以,E、F、G、H四点共面.
-------------------------5分
(2)由(1)可知,EH∥FG
,且EH FG,即EF,GH是梯形的两腰,所以它们的延长线必相交于一点, 设这个交点为P.
FG,即EF,GH是梯形的两腰,所以它们的延长线必相交于一点, 设这个交点为P.
∵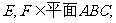 ∴
∴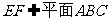 ∵
∵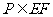 ∴
∴
同理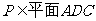 , ∵
, ∵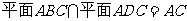 , ∵
, ∵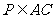
所以EF, GH, AC交于一点 ----------------------------------------------11分
7. 解: (1)由已知可求得AB所在直线的斜率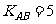 ,
--------------2分
,
--------------2分
因为AB⊥CH, 所以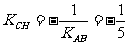
,所以直线CH的方程为: 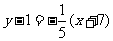 , 整理得:
, 整理得: 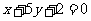 ---------------------5分
---------------------5分
(2) AB边 的中点M坐标为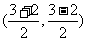 即为
即为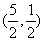 -------------------------------------7分
-------------------------------------7分
所以直线CM的方程为: 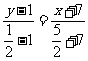 , 整理得:
, 整理得: 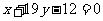 -------------10分
-------------10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com