
题目列表(包括答案和解析)
10.(本小题满分12分)
解:V=336+100 ,(6分) S=360+100
,(6分) S=360+100 (6分)
(6分)
9. (本小题满分12分)
(本小题满分12分)
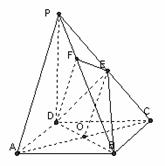
解:(1)证明:连结AC,AC交BD于O.连结EO.
∵ 底面ABCD是正方形,∴ 点O是AC的中点.
在△PAC中,EO是中位线,∴ PA//EO.
而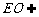 平面EDB,且
平面EDB,且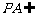 平面EDB,
平面EDB,
所以,PA//平面EDB. ……6分
(2)证明:∵
PD⊥底面ABCD,且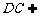 底面ABCD,
∴ PD⊥DC.
底面ABCD,
∴ PD⊥DC.
∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC.
而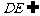 平面PDC,∴
BC⊥DE.
平面PDC,∴
BC⊥DE.
又∵PD=DC,E是PC的中点,∴ DE⊥PC. ∴ DE⊥平面PBC.
而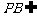 平面PBC,
平面PBC,
∴ DE⊥PB.又EF⊥PB,且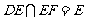 ,∴PB⊥平面EFD.……12分
,∴PB⊥平面EFD.……12分
8. (本小题满分10分)
(本小题满分10分)
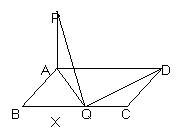
解:假设在BC边上存在点Q,使得PQ⊥QD,(2分)
因为PA⊥平面ABCD,所以PA⊥QD,又由于PQ⊥QD,
所以QD⊥平面APQ,则QD⊥AQ,即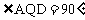 ,
,
易得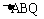 ∽
∽ ,设BQ=X,所以有X(a-X)=1
,设BQ=X,所以有X(a-X)=1
即:x2-ax+1=0
所以当 =a2-4
=a2-4 0时,上方程有解,(8分)
0时,上方程有解,(8分)
因此,当a 2时,存在符合条件的点Q,否则不存在。 ……10分
2时,存在符合条件的点Q,否则不存在。 ……10分
7.(本小题满分10分)
解:(1)如图,延长MP、A/B/相交于点E,连结NE,交B/C/于Q,
连结QP,则NE为平面MNP与平面A/B/C/D/的交线,PQ为平面MNP
与平面BB/C/C的交线;
理由: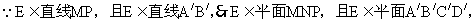
同理,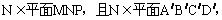 所以,NE为平面MNP与平面A/B/C/D/的交线,
所以,NE为平面MNP与平面A/B/C/D/的交线,
显然,PQ为平面MNP与平面BB/C/C的交线;(5分)
(2)由已知和(1)得MB=B/E=4,又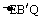 ∽
∽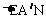 ,所以,B/Q=
,所以,B/Q=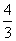 ,又B/P=4,
,又B/P=4,
所以,PQ=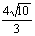 (5分)
(5分)
6.(本题满分14分)若不等式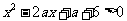 在
在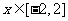 时总成立,求实数
时总成立,求实数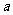 的取值范围.
的取值范围.
思路:令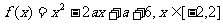 ,,
………………………1分
则
,,
………………………1分
则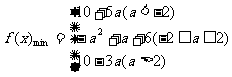 ………………………7分
椐题意知由
………………………7分
椐题意知由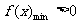 ………………………10分
得
………………………10分
得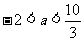 .
………………………14分
.
………………………14分
5.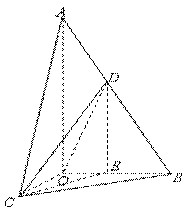 (本题满分14分)如图,在
(本题满分14分)如图,在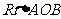 中,
中,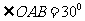 ,斜边
,斜边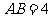 .
. 可以通过
可以通过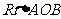 以直线
以直线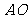 为轴旋转得到,且二面角
为轴旋转得到,且二面角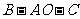 是直二面角.动点
是直二面角.动点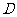 的斜边
的斜边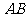 上.
上.
(1)求证: 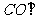 平面
平面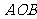 ;
;
(2)当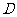 为
为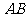 的中点时,求异面直线
的中点时,求异面直线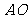 与
与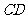 所成角的正切值;
所成角的正切值;
(3)求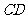 与平面
与平面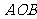 所成的角最大时的正切值.
所成的角最大时的正切值.
(1)由题意,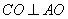 ,
,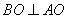 ,
,
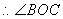 是二面角
是二面角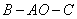 是二面角的平面角,--------------------1
是二面角的平面角,--------------------1
又 二面角
二面角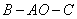 是直二面角,
是直二面角,
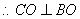 ,又
,又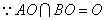 ,
, 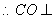 平面
平面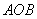 --------------4
--------------4
(2)作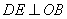 ,垂足为
,垂足为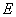 ,连结
,连结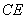 ,在平面
,在平面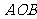 中,则
中,则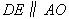 ,
,
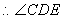 是异面直线
是异面直线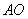 与
与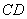 所成的角.--------------------------6
所成的角.--------------------------6
在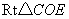 中,
中,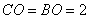 ,
,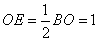 ,
,
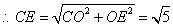 . 又
. 又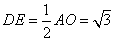
 在
在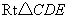 中,
中,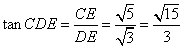 .
.
异面直线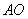 与
与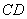 所成角的正切值为
所成角的正切值为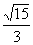 -----------------------9
-----------------------9
(3)由(I)知,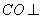 平面
平面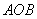 ,
,
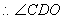 是
是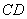 与平面
与平面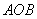 所成的角,且
所成的角,且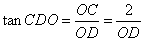
当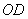 最小时,
最小时,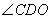 最大, ----------12
最大, ----------12
这时,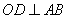 ,垂足为
,垂足为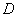 ,,
,,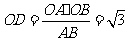
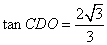 ,
,
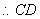 与平面
与平面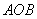 所成的角最大时的正切值为
所成的角最大时的正切值为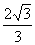 .---------------------14
.---------------------14
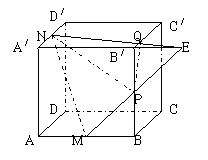
4.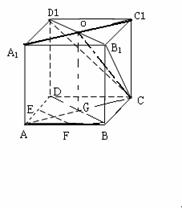 (本题满分14分)如图,正方体
(本题满分14分)如图,正方体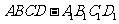 中,
中,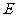 、
、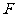 为棱
为棱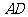 、
、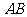 的中点(1)求证:
的中点(1)求证: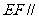 平面
平面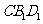
(2)求证:平面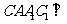 平面
平面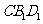
(1)连接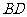 ,在正方体中,
,在正方体中,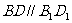 ,-------------.1ˊ
,-------------.1ˊ
又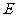 、
、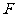 为棱
为棱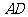 、
、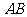 的中点,
的中点,
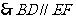
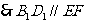 , ---------3ˊ
, ---------3ˊ
又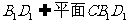 ,
,
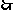
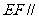 平面
平面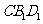 ---------------------------5ˊ
---------------------------5ˊ
(2)在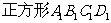 中,
中,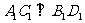 ,又由正方体中
,又由正方体中 ,
,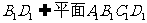
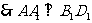 -----------------------------------------------.2
-----------------------------------------------.2
又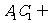
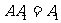 ,
,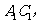
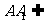 平面
平面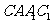
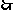
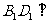 平面
平面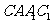 ---------4
---------4
又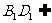 平面
平面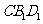
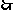 平面
平面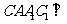 平面
平面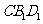 -------------------------------5
-------------------------------5
(3)  平面
平面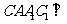
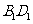 ,设O、G分别是上、下底面中心,连接OG、CO则有
,设O、G分别是上、下底面中心,连接OG、CO则有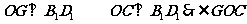 二面角
二面角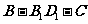 的平面角
的平面角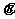 ,-----------2
,-----------2
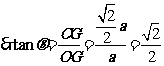 (设
(设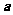 为正方形的边长)
-------------------------------------------4
为正方形的边长)
-------------------------------------------4
3、(本小题14分) 如图:已知平面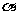 //平面
//平面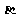 ,点A、B在平面
,点A、B在平面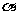 内,点C、D在
内,点C、D在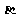 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,求证:(Ⅰ)E、F、G、H四点共面;(Ⅱ)平面EFGH//平面
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,求证:(Ⅰ)E、F、G、H四点共面;(Ⅱ)平面EFGH//平面 .
.
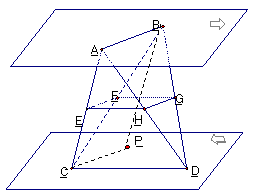 证:(Ⅰ)∵点E、F是线段AC、BC的中点,
证:(Ⅰ)∵点E、F是线段AC、BC的中点,
∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH, 因此: E、F、G、H四点共面;
---------- ---------------------------------4
(Ⅱ)∵平面 //平面
//平面 ,点A、B在平面
,点A、B在平面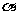 内,
内,
∴AB//平面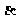 设平面ABC与平面
设平面ABC与平面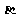 的交线为CP,
的交线为CP,
∵直线AB与CD是异面直线,
∴CP与CD必定相交,∵AB//平面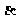 , ∴AB//CP,
, ∴AB//CP,
又EF∥AB, ∴EF//CP,∴EF∥平面 ,-------------------------------------------------.9
,-------------------------------------------------.9
∵点E、H是线段AC、AD的中点,∴EH∥CD, ∴EH∥平面 ,---------------.11
,---------------.11
因此:平面EFGH//平面 .-------------------------------------------------------------------.14
.-------------------------------------------------------------------.14
2. (本小题12分)下图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积

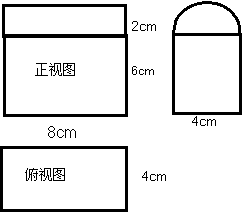 解:此几何体是一个组合体,下
解:此几何体是一个组合体,下
半部是直四棱柱,上半部是半圆柱,
其轴截面的大小与四棱柱的上底
面大小一致。
表面积为S。则
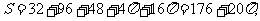
体积为V,则
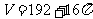 ,
,
所以几何体的的表面积为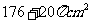 ,
,
体积为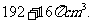
1.(本小题12分)已知函数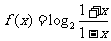 ,
,
1)求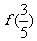 和
和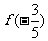 ;
;
2)判断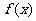 的奇偶性,并说明理由。
的奇偶性,并说明理由。
解:(1)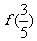 =2
=2 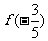 =-2
=-2
(2) 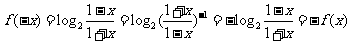
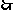
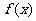 为奇函数
为奇函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com