
题目列表(包括答案和解析)
6.解: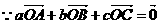 ∴
∴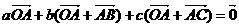
∴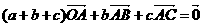 ∴
∴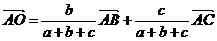
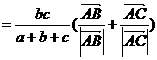
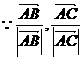 分别是
分别是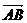 和
和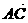 方向上的单位向量,设
方向上的单位向量,设 ,则
,则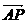 平分
平分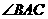 ,又
,又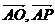 共线,知
共线,知 平分
平分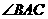 ,同理可证:
,同理可证: 平分
平分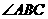 ,
, 平分
平分 ,从而
,从而 是
是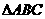 的内心
的内心
5.解: ,∴
,∴
∴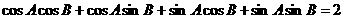 即
即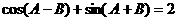
∴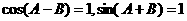 ∴
∴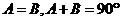 ,∴
,∴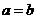 ,
,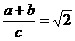 ,故选B
,故选B
4.解法一: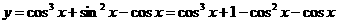
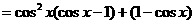
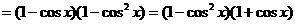
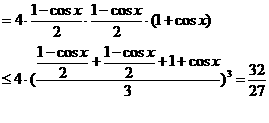 ,∴
,∴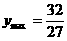 ,故选A
,故选A
解法二: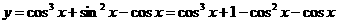
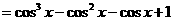 ,令
,令 ,则
,则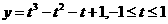
令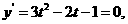 得
得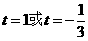
当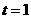 时,
时,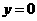 ;当
;当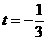 时,
时,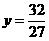 ,∴
,∴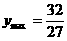 ,故选A
,故选A
3.解法一:令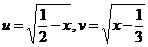 ,则
,则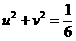 ,而
,而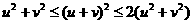
所以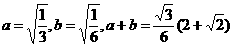 ,故答案选D.
,故答案选D.
解法二:设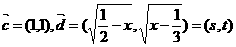 ,
,
则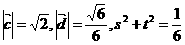 ,
,
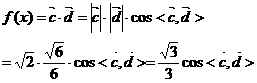
又图可知: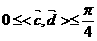 ,∴
,∴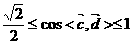 ,∴
,∴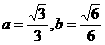
∴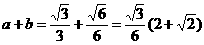 ,故选D.
,故选D.
2. 解: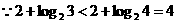 ∴
∴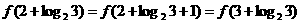
又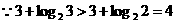 ∴
∴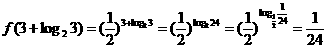
所以答案选D
1.解:当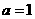 时,
时,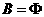 ,满足条件
,满足条件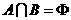
当 时,
时,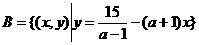 ,欲使
,欲使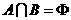 ,则只需满足以下两种情形中的一种即可:(1).斜率相等,即
,则只需满足以下两种情形中的一种即可:(1).斜率相等,即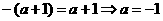
(2).交点为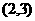 ,则
,则 ,解得
,解得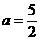 或
或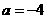 ,综上选(D)
,综上选(D)
15.证明:(1)若x>0,y>0,则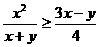 ;
;
(2) 若x,y,z∈R+,则 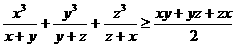 。
。
13设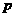 与
与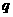 为正整数,满足:
为正整数,满足:
求证: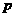 可被1979整除
可被1979整除
14.设 求
求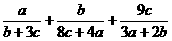 的最小值
的最小值
12.若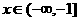 ,不等式
,不等式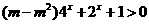 恒成立,则实数
恒成立,则实数 的取值范围是_______
的取值范围是_______
11.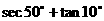 的值是____________
的值是____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com