
题目列表(包括答案和解析)
4. 下列两个变量之间的关系哪个不是函数关系( )
A﹒圆的半径和该圆的周长 B﹒角度和它的正弦值
 C﹒人的年龄和他的身高
D﹒正多边形的边数和它的内角和
C﹒人的年龄和他的身高
D﹒正多边形的边数和它的内角和
3. 某校共有高中学生1000人,其中高一年级400人,高二年级340人,高三年级260人,现采用分层抽样抽取容量为50的样本,那么高一、高二、高三各年级抽取人数分别为( )
A.20、17、13 B.20、15、15
C.40、34、26 D.20、20、10
2.已知 且
且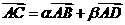 ,则( )
,则( )
A.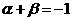 B.
B.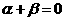 C.
C.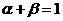 D.
D.
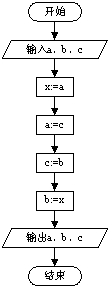
1. 下列程序框能表示赋值、计算功能的是( )

A﹒ B﹒ C﹒ D
20. (本小题满分16分)
已知函数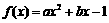 .
.
(1)若不等式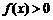 的解集是
的解集是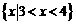 ,求a,b的值;
,求a,b的值;
(2)当b=2时,若不等式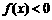 对一切实数x恒成立,求a的取值范围;
对一切实数x恒成立,求a的取值范围;
(3)当a=1时,设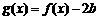 ,若存在
,若存在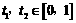 ,使得
,使得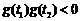 成立,求b的取值范围.
成立,求b的取值范围.
19. (本小题满分16分)
(1)设集合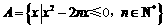 ,其元素个数记为an.
,其元素个数记为an.
①求an,并且证明{an}是等差数列;
②设Sn为{an}的前n项和,m、k、p∈N*,且满足m+p=2k,求证: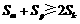 ;
;
(2)对于(1)②中的命题,对各项均为正数的等差数列还成立吗?如果成立,请证明你的结论;如果不成立,请说明理由.
18. (本小题满分16分)
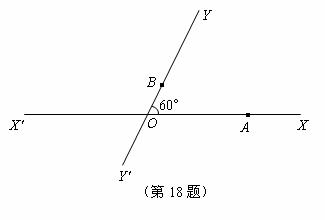
如图,有两条相交成60°的直路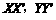 ,交点是O. 甲、乙两人分别在OX,OY上,起初甲在离O点3km的A处,乙在离O点1km的B处. 后来甲沿
,交点是O. 甲、乙两人分别在OX,OY上,起初甲在离O点3km的A处,乙在离O点1km的B处. 后来甲沿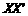 的方向,乙沿
的方向,乙沿 的方向,同时以4km/h的速度步行.
的方向,同时以4km/h的速度步行.
(1)起初两人的距离是多少?
(2)t h后两人的距离是多少?
(3)何时两人的距离最短?
17. (本小题满分14分)
在一次招聘会的面试中,每位应聘者在8道面试试题中随机抽取2道题回答,若至少答对其中1题即为及格.
(1)某应聘者会答8道题中的5道题,求该应聘者及格的概率;
(2)若一位应聘者及格的概率小于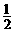 ,则他最多会答几道题?
,则他最多会答几道题?
16. (本小题满分14分)
已知正数m,n满足5m+2n=20.
(1)求lgm+lgn的最大值,并求出取得最大值时的m,n的值;
(2)求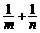 的最小值.
的最小值.
15. (本小题满分14分)
某高级中学共有学生3 000名,各年级男、女生人数如下表:
|
|
高一年级 |
高二年级 |
高三年级 |
|
女生 |
523 |
x |
y |
|
男生 |
487 |
490 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.
(1)问高二年级有多少名女生?
(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com