
题目列表(包括答案和解析)
9.一个正四棱台的上、下底面边长分别为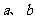 ,高为
,高为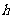 ,且侧面积等于两底面积之和,则下列关系正确的是
,且侧面积等于两底面积之和,则下列关系正确的是
A.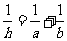 B.
B.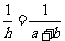 C.
C.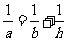 D.
D.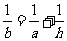
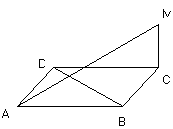
8.如图,如果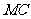 ⊥菱形
⊥菱形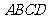 所在的平面,
所在的平面,
那么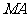 与
与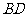 的位置关系是
的位置关系是
A.平行 B.垂直相交
C.异面 D.相交但不垂直
7.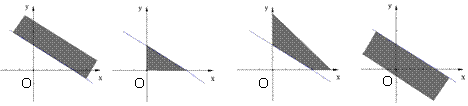 不等式
不等式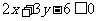 表示的平面区域是
表示的平面区域是
A. B. C. D.
6.直线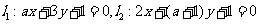 , 若
, 若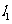 ∥
∥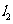 ,则
,则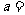
A. B.
B.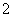 C.
C. 或
或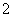 D.
D.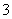 或
或
5.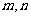 是两条不同直线,
是两条不同直线,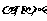 是三个不同平面,下列命题中正确的是
是三个不同平面,下列命题中正确的是
A.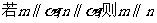 B.
B.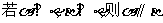
C.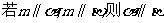 D.
D.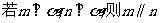
4.有下列四个命题:(1)过三点确定一个平面;(2)矩形是平面图形;(3)三条直线两
两相交则确定一个平面;(4)两个相交平面把空间分成四个区域其中错误命题的序号是
A.(1)和(2) B.(1)和(3)) C.(2)和(4) D.(2)和(3)
3.若一个几何体的主视图和侧视图都是等腰梯形,则这个几何体可能是
A.圆柱 B.棱锥 C.球体 D.圆台
2.点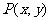 在直线
在直线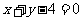 上,
上,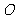 是坐标原点,则
是坐标原点,则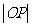 的最小值是
的最小值是
A.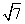 B.
B.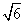 C.
C.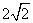 D.
D.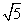
1.若直线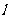 经过原点和点
经过原点和点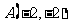 ,则它的斜率为
,则它的斜率为
A.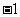 B.
B.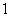 C.
C.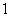 或
或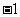 D.
D.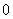
15.(本题满分7分)某工厂生产甲、乙两种产品.甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%.生产1件甲产品若是一等品则获利4万元,若是二等品则亏损1万元;生产1件乙产品若是一等品则获利6万元,若是二等品则亏损2万元.设生产各件产品相互独立.
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的总利润不少于10万元的概率.
解:(1)由题设知X的可能取值为10,5,2, .且
.且
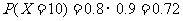 ,
,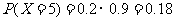 ,
,
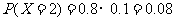 ,
, 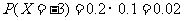 .
.
由此得X的分布列为
|
X |
 |
2 |
5 |
10 |
|
P |
0.02 |
0.08 |
0.18 |
0.72 |
(2)设生产的4件甲产品中一等品n件,则二等品有 件.
件.
由题设知 解得
解得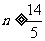 .
.
又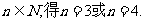
所以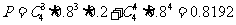
 所求概率为0.8192
所求概率为0.8192
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com