
题目列表(包括答案和解析)
11.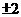 12,1 13.
12,1 13. 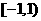 14.-8 15.-8
14.-8 15.-8
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
A |
C |
B |
C |
B |
C |
D |
A |
B |
21.(本小题14分)设函数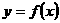 定义在
定义在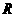 上,对于任意实数
上,对于任意实数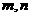 ,恒有
,恒有
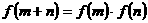 ,且当
,且当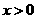 时,
时,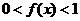
(1)求证: 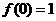 且当
且当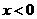 时,
时,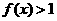
(2)求证: 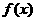 在
在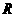 上是减函数;
上是减函数;
(3)设集合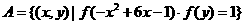 ,
,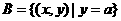 ,
,
且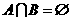 , 求实数
, 求实数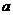 的取值范围。
的取值范围。
20.(本题满分14分)
探究函数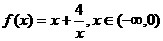 的最大值,并确定取得最大值时
的最大值,并确定取得最大值时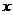 的值.列表如下:
的值.列表如下:
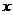 |
… |
-0.5 |
-1 |
-1.5 |
-1.7 |
-1.9 |
-2 |
-2.1 |
-2.2 |
-2.3 |
-3 |
… |
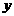 |
… |
-8.5 |
-5 |
-4.17 |
-4.05 |
-4.005 |
-4 |
-4.005 |
-4.02 |
-4.04 |
-4.3 |
… |
请观察表中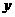 值随
值随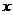 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
函数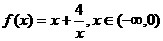 在区间
在区间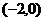 上递减;
上递减;
(1)函数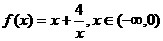 在区间
上递增.
在区间
上递增.
当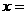 时,
时,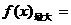 .
.
(2)证明:函数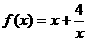 在区间
在区间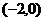 递减.
递减.
(3)思考:函数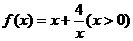 有最大值或最小值吗?如有,是多少?此时
有最大值或最小值吗?如有,是多少?此时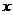 为何值?(直接回答结果,不需证明).
为何值?(直接回答结果,不需证明).
19. (本题满分13分)
已知函数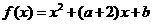 满足
满足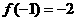 ;
;
(1)若方程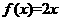 有唯一的解;求实数
有唯一的解;求实数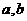 的值;
的值;
(2)若函数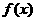 在区间
在区间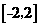 上不是单调函数,求实数
上不是单调函数,求实数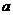 的取值范围。
的取值范围。
18.(本题满分13分)已知集合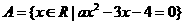 ,
,
(1)若 中有两个元素,求实数
中有两个元素,求实数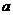 的取值范围;
的取值范围;
(2)若 中至多有一个元素,求实数
中至多有一个元素,求实数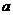 的取值范围.
的取值范围.
17.(本题满分13分)已知函数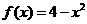
(1)试判断函数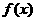 的奇偶性,并证明函数
的奇偶性,并证明函数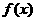 在
在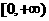 是减函数;
是减函数;
(2)解不等式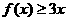 .
.
16.计算:(本题满分13分)
设全集为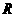 ,集合
,集合 =
=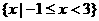 ,
,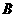 =
=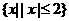 ,
,
(1)求: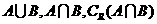 ;
;
(2)若集合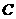
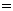
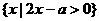 ,满足
,满足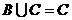 ,求实数
,求实数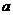 的取值范围。
的取值范围。
15.已知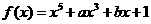 且
且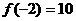 ,那么
,那么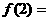
14.奇函数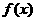 在区间
在区间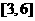 上是增函数且最大值为
上是增函数且最大值为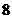 , 则函数
, 则函数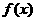 在区间
在区间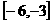 上的最小值为___
上的最小值为___
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com