
题目列表(包括答案和解析)
7.正方体的内切球和外接球的半径之比为( )
A. 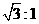 B.
B. 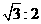 C.
C. 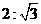 D.
D. 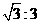
6.长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是
A、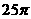 B、
B、 C、
C、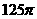 D、都不对
D、都不对
5.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后 ,剩下的几何体的体积是( )
A. 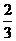 B.
B. 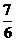 C.
C. 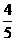 D.
D. 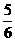
4.有一个几何体的三视图如下图所示,这个几何体应是一个
|
|
|

A、棱台 B、棱锥 C、棱柱 D、都不对
3、一个棱柱是正四棱柱的条件是
A、底面是正方形,有两个侧面是矩形
B、底面是正方形,有两个侧面垂直于底面
C、底面是菱形,且有一个顶点处的三条棱两两垂直
D、每个侧面都是全等矩形的四棱柱
2、半径为R的半圆卷成一个圆锥,则它的体积为( )
A. 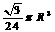 B.
B. 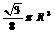 C.
C. 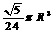 D.
D. 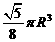
1、如果一个水平放置的图形的斜二测直观图是一个底面为45o ,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A. 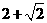 B.
B. 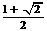 C.
C. 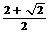 D.
D. 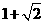
19.(本题满分12分)
学习立体几何时常与平面几何进行类比.
(1)对平面几何中的勾股定理:“在Rt△ABC中,AB是斜边,则有AB2=AC2+BC2”类比可得:在三棱锥P-ABC中,PA⊥PB,PB⊥PC,PC⊥PA,则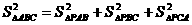 ,试证明该结论成立.
,试证明该结论成立.
(2)对平面几何中“正三角形内任一点到三边的距离之和为定值”的结论进行类比,在立体几何你能得到什么样的结论(不须证明).
18.(本题满分12分)
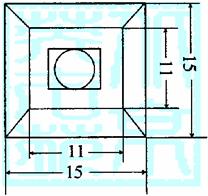
右图是一个将杯的三视图.
(1)请你指出奖杯是由怎样的几何体组成的?
(2)要将奖杯表面镀金,根据图中给出的尺寸,求出该奖杯的表面积(焊接处对面积的影响忽略不计,
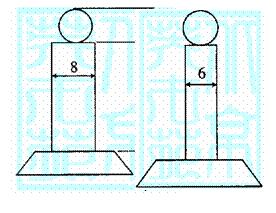 单位:cm)
单位:cm)
17.(本题满分10分)
如图,E、F分别是正方形ABCD的边BC,CD的中点,沿图中虚线折成一个几何体,
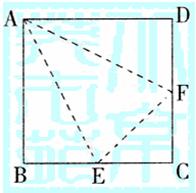 (1)能围成怎样的几何体?
(1)能围成怎样的几何体?
(2)设正方形边长为2,
求所围成几何体的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com