
题目列表(包括答案和解析)
1.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
A.都平行 B.都相交 C.在两个平面内 D.至少和其中一个平行
3.三角恒等式的证明
证明三角恒等式的过程,实际上是化异为同的过程,即化去形式上的异,而呈现实质上的同,这个过程,往往是从化简开始的--这就是说,在证明三角恒等式时,我们可以从最复杂处开始.
例5 求证 cosα(2secα+tgα)(secα-2tgα)=2cosα-3tgα.
分析 从复杂的左边开始证得右边.
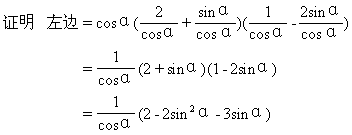
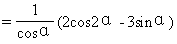
=2cosα-3tgα=右边
例6 证明恒等式
(1)1+3sin2αsec4α+tg6α=sec6α
(2)(sinA+ secA)3+(cosA+cscA)2=(1+secAcscA)2
分析 (1)的左、右两边均较复杂,所以可以从左、右两边同时化简
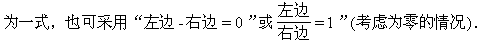
证明 (1)右边-左边=sec6α-tg6α-3sin2αsec4α-1
=(sec2α-tg2α)(sec4α+sec2α·tg2α+tg2α)-3sin2αsec4α-1
=(sec4α-2sec2αtg2α+tg2α)-1
=(sec2α-tg2α)2-1=0
∴等式成立.
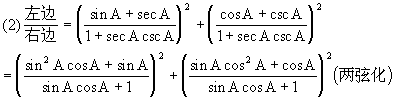
=sin2A+cos2A=1故原式成立
在解题时,要全面地理解“繁”与“简”的关系.实际上,将不同的角化为同角,以减少角的数目,将不同的函数名称,化为同名函数,以减少函数的种类,都是化繁为简,以上两点在三角变换中有着广泛的应用.
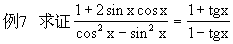
分析1 从右端向左端变形,将“切”化为“弦”,以减少函数的种类.
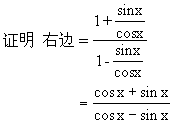
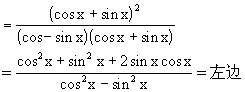
分析2 由1+2sinxcosx立即想到(sinx+cosx)2,进而可以约分,达到化简的目的.
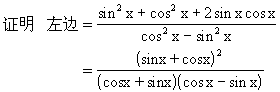
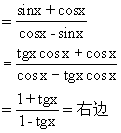
说明 (1)当题目中涉及多种名称的函数时,常常将切、割化为弦(如解法1),或将弦化为切(如解法2)以减少函数的种类.
(2)要熟悉公式的各种变形,以便迅速地找到解题的突破口,请看下列.
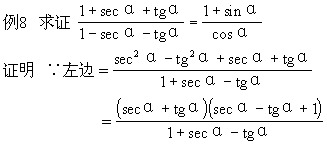
=secα+tgα
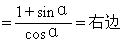
∴等式成立
说明 以上证明中采用了“1的代换”的技巧,即将1用sec2α-tg2α代换,可是解题者怎么会想到这种代换的呢?很可能,解题者在采用这种代换时,已经预见到代换后,分子可以因式分解,可以约分,而所有这一切都是建立在熟悉公式的各种变形的基础上的,当然,对不熟练的解题者而言,还有如下的“一般证法”--即证明“左边-右边=0”
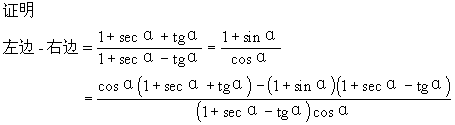
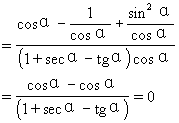
∴左边=右边
2.三角函数式的化简
三角函数式的化简的结果应满足下述要求:
(1)函数种类尽可能地少.
(2)次数尽可能地低.
(3)项数尽可能地少.
(4)尽可能地不含分母.
(5)尽可能地将根号中的因式移到根号外面来.
化简的总思路是:尽可能地化为同类函数再化简.
例3 化简sin2α·tgα+cos2α·ctgα+2sinαcosα
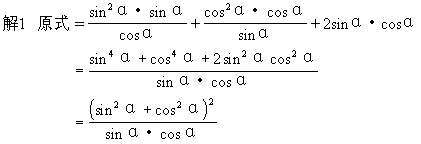
=secα·cscα
解2 原式=(sin2α·tgα+sinα·cosα)+(cos2α·ctgα+sinαcosα)
=tgα·(sin2α+cos2α)+ctgα(sin2α+cos2α)
=tgα+ctgα
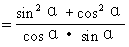
=secα·cscα
说明 (1)在解1中,将正切、余切化为正弦、余弦再化简,仍然是循着减少函数种类的思路进行的.
(2)解2中的逆用公式将sinα·cosα用tgα表示,较为灵活,解1与解2相比,思路更自然,因而更实用.
例4 化简:
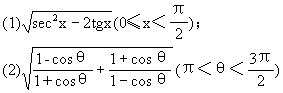
分析 将被开方式配成完全平方式,脱去根号,进行化简.
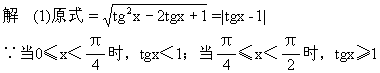
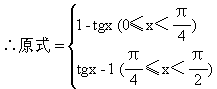
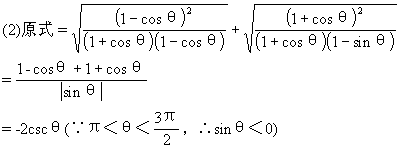
1.已知某角的一个三角函数值,求该角的其他三角函数值.
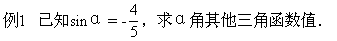
解 ∵sinα<0
∴角α在第三或第四象限(不可能在y轴的负半轴上)
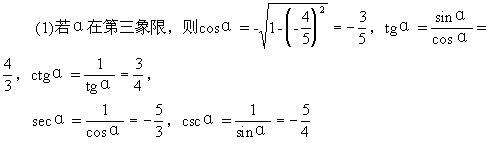
(2)若α在第四象限,则
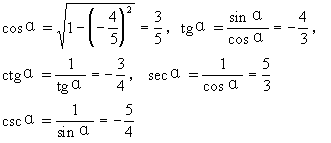
说明 在解决此类问题时,要注意:
(1)尽可能地确定α所在的象限,以便确定三角函数值的符号.
(2)尽可能地避免使用平方关系(在一般情况下只要使用一次).
(3)必要时进行讨论.
例2 已知sinα=m(|m|≤1),求tgα的值.
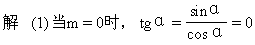
(2)当m=±1时,α的终边在y轴上,tgα无意义.
(3)当α在Ⅰ、Ⅳ象限时,∵cosα>0.
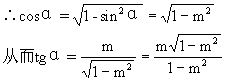
当α在第Ⅱ、Ⅲ象限时,∵cosα<0,
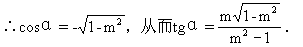
说明 (1)在对角的范围进行讨论时,不可遗漏终边在坐标轴上的情况.
(2)本题在进行讨论时,为什么以cosα的符号作为分类的标准,而不按sinα的符号(即m的符号)来分类讨论呢?你能找到这里的原因并概括出所用的技巧吗?
2.5 指数·例题解析
[例1]若a、b∈R,x、y均为正实数,判断下列运算是否成立:
(1)ax·ay=ax+y; (2)(ax)y=axy;

都没有意义.
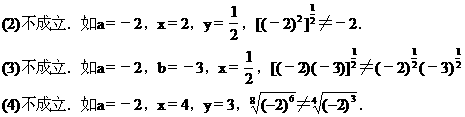
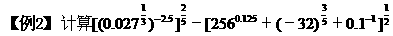
分析 这是幂值的计算问题,一般先把幂化为底数是质数的指数式,再应用同底的幂的运算法则进行计算,有“方向”性,较为方便.
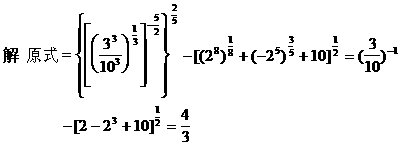
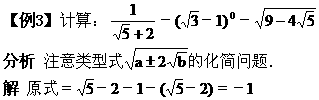
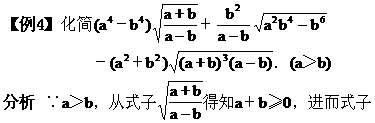
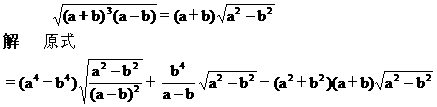
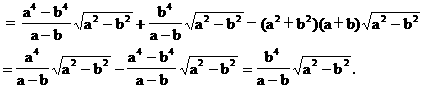
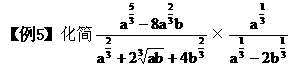
分析 在指数运算中,改变指数结构的表达形式:如a-8b=
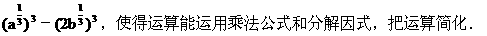
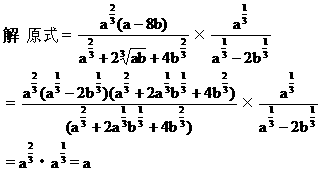

分析 在例5中已谈到改变指数表达形式,除此之外还可用平方法

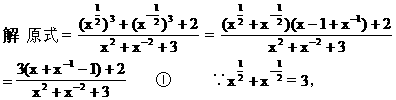

20、(本小题满分14分)已知函数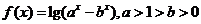
(1)求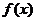 的定义域;
的定义域;
(2)在函数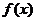 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于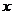 轴;
轴;
(3)当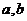 满足什么条件时,
满足什么条件时,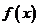 在
在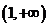 上恒取正值.
上恒取正值.
2010-2011学年度第一学期
19、(本小题满分为14分)定义在(-1,1)上的函数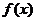 满足:
满足:
①对任意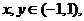 都有
都有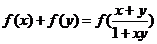 ;
;
②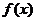 在
在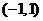 上是单调递增函数,
上是单调递增函数,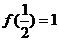 .
.
(1)
求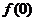 的值;
的值;
(2) 证明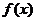 为奇函数;
为奇函数;
(3) 解不等式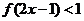 .
.
18.(本小题满分13分).某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是: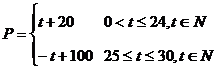
该商品的日销售量Q(件)与时间(天)的函数关系是:Q=-t+40
(0<t≤30,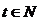 ),
),
求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
17、(本小题满分13分)已知函数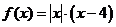
(1) 画出函数的图象;
(2) 利用图象回答:当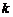 为何值时,方程
为何值时,方程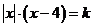 有一个解?有两个解?有三个解?
有一个解?有两个解?有三个解?
16、(本小题满分13分)计算下列各式的值
⑴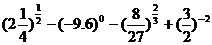 ;
;
⑵ 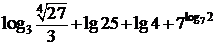 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com