
3.已知空气的单位体积质量是0.001239g/cm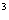 ,用科学计数法表示0.001239(结果保留2位有效数字)正确的是
,用科学计数法表示0.001239(结果保留2位有效数字)正确的是
A.0.124×10-2 B.1.2×10-3 C.1.2×10-2 D.1.2×10-3
2.在下列长度的各组线段中,是勾股数的一组为
A.4,5,6 B.0.3,0.4,0.5 C.1,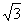 ,2 D.6,8,10
,2 D.6,8,10
1.在下列各式-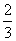 x,
x,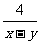 , x+y,
, x+y,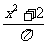 ,
,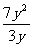 ,
,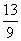 中,分式有
中,分式有
A.1个 B.2个 C.3个 D.4个
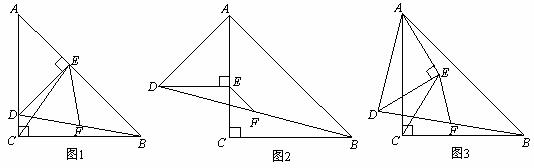
25.如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上, F是线段BD的中点,连结CE、FE.
(1)请你探究线段CE与FE之间的数量关系(直接写出结果,不需说明理由);
(2)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连结BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由;
(3)将图1中的△AED绕点A顺时针旋转任意的角度(如图3),连结BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由.
24.在平面直角坐标系xOy中,抛物线 y=-x2+bx+c与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,顶点为D,且点B的坐标为(1,0), 点C的坐标为(0,3).
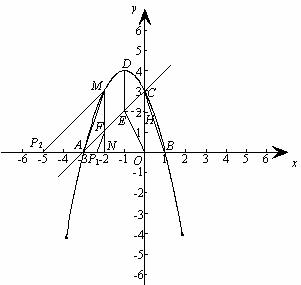
(1)求抛物线及直线AC的解析式;
(2)E、F是线段AC上的两点,且∠AEO=∠ABC,过点F作与y轴平行的直线交抛物线于点M,交x轴于点N.当MF=DE时,在x轴上是否存在点P,使得以点P、A、F、M为顶点的四边形是梯形? 若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q是位于抛物线对称轴左侧图象上的一点,试比较锐角∠QCO与∠BCO 的大小(直接写出结果,不要求写出求解过程,但要写出此时点 Q的横坐标x的取值范围).
23.已知以x为自变量的二次函数y=x2+2mx+m-7.
(1)求证:不论m为任何实数,二次函数的图象与x轴都有两个交点;
(2)若二次函数的图象与x轴的两个交点在点(1,0)的两侧,关于x的一元二次方程m2x2+(2m+3)x+1=0有两个实数根,且m为整数,求m的值;
(3)在(2)的条件下,关于x的另一方程 x2+2(a+m)x+2a-m2+6 m-4=0 有大于0且小于5的实数根,求a的整数值.
22.(本小题满分5分)
如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
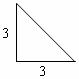

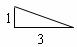




图1 图2 图3
21.(本小题满分5分)列方程或方程组解应用题:
在学校开展的为偏远贫困地区的少年儿童捐献文具的活动中,甲、乙两班共捐献文具260件,已知甲班有40人参加了此次活动,乙班有35人参加了此次活动,且乙班人均捐献文具的件数是甲班人均捐献文具件数的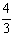 倍,问甲、乙两班各捐献文具多少件?
倍,问甲、乙两班各捐献文具多少件?
19.(本小题满分5分)
已知:如图,AB是⊙O的直径,E是AB延长线上的一点,D是⊙O上的一点,且AD平分∠FAE,ED⊥AF交AF的延长线于点C.
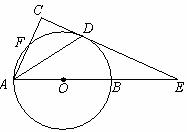
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AF∶FC=5∶3,AE=16,求⊙O的直径AB的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com