
20.(本题满分18分,共有3个小题,第1小题4分,第2小题6分,第3小题8分.)
设向量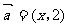 ,
,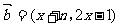 (
(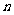 为正整数),函数
为正整数),函数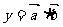 在
在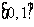 上的最小值与最大值的和为
上的最小值与最大值的和为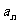 ,又数列
,又数列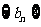 满足:
满足:
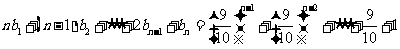 .
.
(1)求证: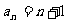 ;
;
(2)求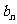 的表达式;
的表达式;
(3)若 ,试问数列
,试问数列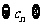 中,是否存在正整数
中,是否存在正整数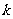 ,使得对于任意的正整数
,使得对于任意的正整数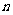 ,都有
,都有 成立?证明你的结论.
成立?证明你的结论.
19.(本题满分16分,共有3个小题,第1小题4分,第2小题5分,第3小题7分.)
已知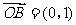 ,直线
,直线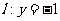 ,动点
,动点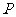 到直线l的距离
到直线l的距离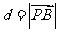
(1)求动点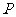 的轨迹方程
的轨迹方程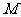 ;
;
(2)证明命题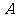 :“若直线
:“若直线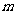 交动点
交动点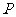 的轨迹
的轨迹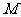 于
于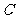 、
、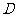 两点,如
两点,如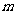 过点
过点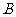 ,则
,则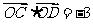 ”为真命题;
”为真命题;
(3)写出命题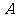 的逆命题,判断该逆命题的真假,并说明理由.
的逆命题,判断该逆命题的真假,并说明理由.
18.(本题满分14分,共有2个小题,第1小题满分6分,第2小题满分8分)
(理)某公司2008年底共有员工200人,当年的生产总值为1600万元.该企业规划从2009年起的10年内每年的总产值比上一年增加100万元;同时为扩大企业规模,该企业平均每年将录取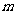 (
(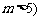 名新员工;经测算,这10年内平均每年有5名员工退休.设从2009年起的第x年(2009年为第1年)该企业的人均产值为y万元.
名新员工;经测算,这10年内平均每年有5名员工退休.设从2009年起的第x年(2009年为第1年)该企业的人均产值为y万元.
(1)写出y与x之间的函数关系式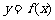 ;
;
(2)要使该企业的人均产值在10年内每年都有增长,则每年录用的新员工至多为多少人?
(文)为了缓解交通压力,某省在两个城市之间特修一条专用铁路,用一列火车作为公共交通车。如果该列火车每次拖4节车厢,每日能来回16趟;如果每次拖7节车厢,则每日能来回10趟。火车每日每次拖挂车厢的节数是相同的,每日来回趟数y是每次拖挂车厢节数x的一次函数,每节车厢满载时能载客110人.
(1)求出y关于x的函数关系式;
(2)这列火车满载时每次应拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数.
17.(本题满分14分,共有2个小题,第1小题满分8分,第2小题满分6分)
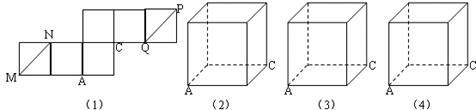
如图,图(1)是一个正方体的表面展开图,MN和PQ是两条面对角线.
(1)请在图(2)的正方体中画出MN、PQ;并求此时MN与PQ所成角的大小;
(2)求四面体MNPQ的体积与正方体的体积之比.
(说明:求角与体积时,若需画辅助图,请分别画在图(3)、(4)中)
16.(本题满分12分)
已知复数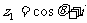 和
和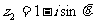 ,求
,求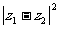 的最大值和最小值.
的最大值和最小值.
15.若函数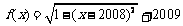 ,则对任意的
,则对任意的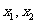 满足
满足
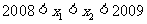 ,
,
则有 ( )
A.)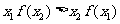 B.
B.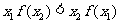 .
.
C.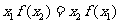 . D.
. D.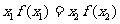
14.将函数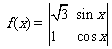 的图像向左平移
的图像向左平移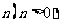 个单位,所得图像对应的函数为偶函数,则
个单位,所得图像对应的函数为偶函数,则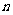 的最小值为 ( )
的最小值为 ( )
A. 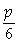 . B.
. B.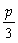 .
C.
.
C.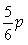 . D.
. D.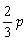
13.若直线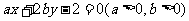 平分圆
平分圆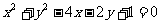 的周长,则
的周长,则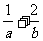 的最小值为 ( )
的最小值为 ( )
A.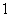 .
B.
.
B.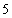 .
C.
.
C.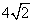 . D.
. D.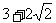 .
.
12.在空间中,“两条直线没有公共点”是“这两条直线异面”的 ( )
A.充分不必要条件. B.必要不充分条件
C.充要条件. D.既不充分也不必要条件
11.若对任意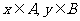 ,(
,(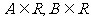 )有唯一确定的
)有唯一确定的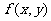 与之对应,则称
与之对应,则称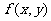 为关于
为关于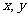 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数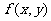 为关于实数
为关于实数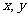 的广义“距离”:
的广义“距离”:
(1)非负性: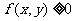 ,当且仅当
,当且仅当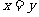 时取等号;
时取等号;
(2)对称性: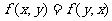 ;
;
(3)三角形不等式: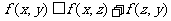 对任意的实数
对任意的实数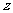 均成立.
均成立.
今给出三个二元函数,请选出所有能够成为关于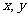 的广义“距离”的序号: .
的广义“距离”的序号: .
①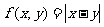 ; ②
; ②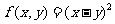 ; ③
; ③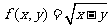 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com