22．(本小题满分14分)

(理)已知A、B、C是直线l上三点，向量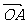、、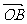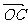满足：

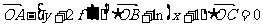，且函数y=f(x)在定义域内可导．

(1)求函数y=f(x)的解析式；　　　

(2)若x>0，证明：f(x)>；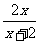

(3)若不等式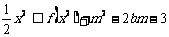对x∈［－1，1］及b∈［－1，1］都恒成立，求实数m的取值范围．

(文)已知函数．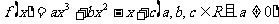

(1)若b=1，且f(x)在(2，+∞)上存在单调递增区间，求a的取值范围；

(2)若存在实数x₁、x₂ (x₁≠x₂)满足f(x_­1)=f(x₂)，是否存在实数a、b、c使f(x)在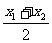处的切线斜率为0？若存在，求出一组实数a、b、c；否则说明理由．

21．(本小题满分12分)

对数列{a_n}，规定{△a_n}为数列{a_n}的一阶差分数列，其中△a_n=a_n+1－a_n(n∈N)．对自然数k，规定{△^ka_n}为{a_n}的k阶差分数列，其中△^ka_n=△^k－1a_n+1－△^k－1a_n=△(△^k－1a_n)．

(1)已知数列{a_n}的通项公式a_n=n²+n (n∈N)，试判断{△a_n}，{△²a_n}是否为等差或等比数列，为什么？

(2)若数列{a_n}首项a₁=1，且满足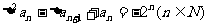，求数列{a_n}的通项公式；

(3)对(2)中数列{a_n}，是否存在等差数列{b_n}，使得b₁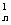C+ b₂C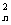+…+ b_nC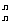= a_n对一切自然n∈N都成立？若存在，求数列{b_n}的通项公式；若不存在，则请说明理由．

20．(本小题满分12分)

如图，椭圆两焦点F₁、F₂与短轴两端B₁、B₂正好是正方形的四个项点，且焦点到椭圆上一点最近距离为．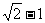

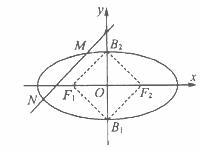
(1)求椭圆的标准方程；

(2)过D (0，2)的直线与椭圆交于不同的两点M、N，且M在D、N之间，设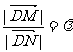，求λ的取值范围．

19．(本题满分12分)

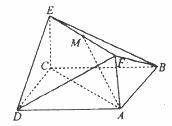
如图，已知正方形ABCD和矩形ACEF所在平面互相垂直，AB=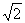，AF=1，M是线段EF的中点．

(1)求证：AM∥平面BDE；　 (2)求二面角A-DF-B的大小；

(3)试问：在线段AC上是否存在一点P，使得直线PF与AD所成角60°

18．(本小题满分12分)

有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一组．

如：密码12213的明文为BEP，设随机变量ξ表示密码中不同数字的个数．

(1)求P(ξ=2)；　　 (2)求随机变量ξ的颁布列和它的数学期望．

17．(本小题满分12分)

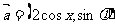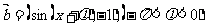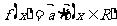已知，．定义，且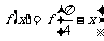对任意实数x恒成立．

(1)求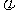的值；　　 (2)求函数的单调增区间．

16．记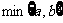 为a、b两数的最小值，当正数x、y变化时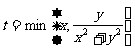，也在变化，则t的最大值为___________．

15．已知(1－x)ⁿ的展开式中所有项的系数的绝对值之和为32，(1－x)ⁿ的展开式中的系数最小的项是______________．

14．已知函数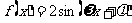(其中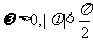)的最小正周期是π，且f(0)=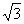，则_______，=________．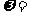

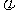13．已知点P(2，1)在圆C：x²+y²+ax－2y+b=0上，点P关于直线x+y－1=0的对称点也在圆C上，则圆C的圆心标为___________、半径为_________．