
2.平面α与平面β外有一条直线m,如果m在α与β内的射影分别是直线m1和直线m2,给出下列四个命题:
①m1∥m2⇒α∥β; ②α∥β⇒m1∥m2;
③α⊥β⇒m1⊥m2; ④α与β相交⇒m1与m2相交;
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
1.函数y=+的定义域为( )
A.{x|x≥1或x≤-1} B.{x|-1≤x≤1} C.{1} D.{-1,1}
22.(本小题12分)
已知数列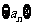 中,
中,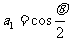
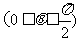 ,
,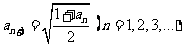 .
.
(Ⅰ)求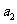 、
、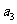 ;
;
(Ⅱ)求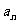 ;
;
(Ⅲ)
设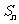 为数列
为数列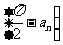 的前n项和,证明:
的前n项和,证明: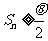 .
.
21.(本小题12分)
已知函数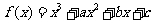 .
.
(Ⅰ)当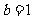 时,若函数
时,若函数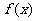 在
在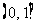 上为增函数,求实数
上为增函数,求实数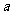 的最小值;
的最小值;
(Ⅱ)设函数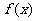 的图像关于原点
的图像关于原点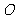 对称,在点
对称,在点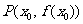 处的切线为
处的切线为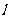 ,
,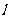 与函数
与函数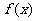 的图像交于另一点
的图像交于另一点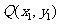 .若
.若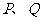 在
在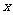 轴上的射影分别为
轴上的射影分别为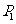 、
、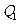 ,
,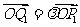 ,求
,求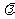 的值.
的值.
20.(本小题12分)
已知双曲线焦点在x轴上、中心在坐标原点O,左、右焦点分别为F1、F2,P为双曲线右支上一点,且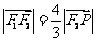 ,
,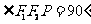 .
.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设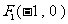 ,过
,过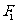 的直线
的直线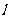 与双曲线的两渐近线分别交于
与双曲线的两渐近线分别交于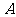 、
、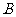 两点,
两点,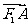 与
与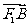 同向,
同向,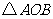 的面积为
的面积为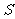 .若
.若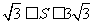 ,求
,求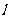 的斜率
的斜率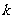 的取值范围.
的取值范围.
19.(本小题12分)
某工厂新开发的一种产品有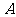 、
、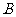 两项技术指标需要检测,设各项技术指标达标与否互不影响.若恰有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若恰有一项技术指标达标的概率为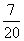 ,至少有一项技术指标达标的概率为
,至少有一项技术指标达标的概率为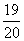 .检验规定两项技术指标都达标的新产品为合格品.
.检验规定两项技术指标都达标的新产品为合格品.
(Ⅰ)求一件新产品经过检测为合格品的概率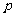 ;
;
(Ⅱ)工厂规定:若每生产一件合格的新产品,该工人将获得奖金100元;若生产一件不合格的新产品,该工人将被罚款50元。该工人一个月能生产新产品20件,求该工人一个月获得奖金的数学期望.
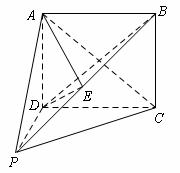
18.(本小题12分)
如图,四棱锥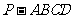 的底面
的底面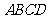 是正方形,
是正方形,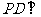 面
面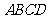 .
.
(Ⅰ)证明:平面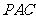
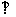 平面
平面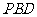 ;
;
(Ⅱ)设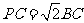 .
.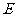 为
为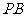 的中点,求二面角
的中点,求二面角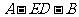 的大小.
的大小.
17.(本小题10分)
在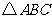 中,
中,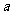 、
、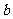 、
、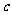 分别是角
分别是角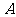 、
、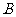 、
、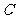 的对边,且
的对边,且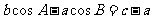 .
.
(Ⅰ)求角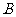 的大小;
的大小;
(Ⅱ)若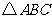 的面积是
的面积是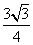 ,且
,且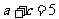 ,求
,求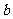 .
.
16.观察以下等式
1=1
3+5=8
7+9+11=27
13+15+17+19=64
… …
写出一个等式,使之既包含以上四式、又具有一般性质。这个等式是:
.
15.某实验室至少需某种化学药品10 kg,现在市场上该药品有两种包装,一种是每袋3 kg,价格为12元;另一种是每袋2 kg,价格为10元.但由于储存的因素,每一种包装购买的数量都不能超过5袋,则在满足需要的条件下,花费最少为 元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com