
9.抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线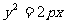
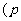 >
>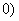 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
A.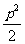 B.
B.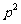 C.
C.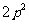 D.
D.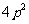
8. 若一个四位数字的数,前两位数字之积恰好等于后面两位数,则称这个数为“吉积数”.如“0900”,“1909”,“9218”等都为“吉积数”。某地汽车牌照某批次的号码前两位是固定的英文字母,后面是四位数字,丁先生买了新车,给汽车上牌照时最多有三次选择机会(有放回地随机选择号码).丁先生选号时刚好是选这批号码的第一位,如果他想选一个末尾数字没有4的“吉积数”,则丁先生成功的最大概率最接近的值为 ( )
A.3% B.1% C.0.88% D.2.64%
7.已知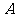 为
为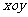 平面内的一个区域.甲:点
平面内的一个区域.甲:点 ;
;
乙:点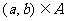 .如果甲是乙的必要条件,那么区域
.如果甲是乙的必要条件,那么区域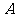 的面积 ( )
的面积 ( )
A.最小值为2 B.无最大值 C.最大值为2 D.最大值为1
6.设A,B两地位于北纬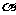 的纬线上,且两地的经度差为
的纬线上,且两地的经度差为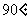 ,若地球的半径为
,若地球的半径为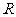 千米,且时速为20千米的轮船从A地到B地最少需要
千米,且时速为20千米的轮船从A地到B地最少需要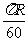 小时,则
小时,则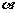 为 ( )
为 ( )
A.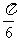 B.
B.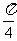 C.
C.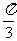 D.
D.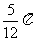
5.已知函数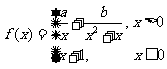 在
在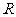 上连续,则
上连续,则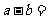 ( )
( )
A.2 B.1 C.0 D.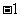
4.已知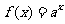 ,
,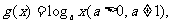 若
若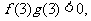 那么
那么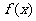 与
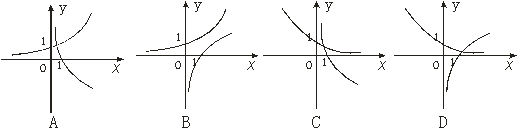
与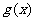 在同一坐标系内的图像可能是 ( )
在同一坐标系内的图像可能是 ( )
3.由一组样本数据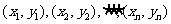 得到的回归直线方程为
得到的回归直线方程为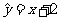 ,且
,且 ,则下列命题中真命题的个数为 ( )
,则下列命题中真命题的个数为 ( )
①直线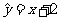 必经过点
必经过点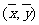 ;
;
②若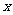 增加一个单位,则
增加一个单位,则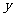 的值估计增加1个单位;
的值估计增加1个单位;
③当相关系数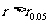 时,
时,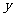 与
与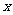 之间具有相关关系.
之间具有相关关系.
A.0 B.1 C.2 D.3
2.已知等比数列{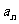 }的前
}的前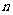 项和为
项和为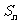 ,且
,且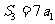 ,则数列
,则数列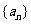 的公比
的公比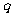 的值为 ( )
的值为 ( )
A.2 B.3 C.2或-3 D.2或3
1.若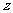 的共轭复数为
的共轭复数为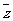 ,
,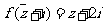 (
(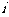 为虚数单位),则
为虚数单位),则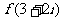 等于 ( )
等于 ( )
A.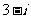 B.
B.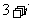 C.
C. D.
D.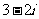
21.(本小题满分14分)
设圆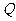 过点
过点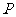 (0,2), 且在
(0,2), 且在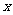 轴上截得的弦
轴上截得的弦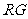 的长为4.
的长为4.
(Ⅰ)求圆心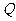 的轨迹
的轨迹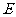 的方程;
的方程;
(Ⅱ)过点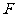 (0,1),作轨迹
(0,1),作轨迹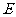 的两条互相垂直的弦
的两条互相垂直的弦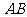 、
、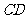 ,设
,设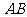 、
、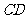 的中点分别为
的中点分别为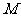 、
、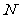 ,试判断直线
,试判断直线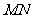 是否过定点?并说明理由.
是否过定点?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com