
19.(本题满分13分)
已知抛物线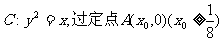 ,作直线
,作直线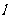 交抛物线于P,Q(点P在第一象限)。
交抛物线于P,Q(点P在第一象限)。
(I)当点A是抛物线C的焦点,且弦长|PQ|=2时,求直线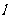 的方程;
的方程;
(II)设点Q关于x轴的对称点M,直线PM交x轴于点B,且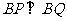 。求证:点B的坐标是(-x0,0),并求点B到直线
。求证:点B的坐标是(-x0,0),并求点B到直线 的距离d的取值范围。
的距离d的取值范围。
18.(本题满分13分)
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如图所示:
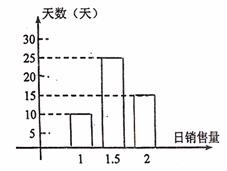
(I)计算这50天的日平均销售量;
(II)若以频率作为概率,且每天的销售量相互独立。
(1)求5天中该种商品恰好有2天的销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,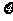 表示该种商品两天销售利润的和(单位:元),求
表示该种商品两天销售利润的和(单位:元),求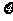 的分布列和数学期望。
的分布列和数学期望。
17.(本题满分13分)
如图,在四棱锥S-ABCD中,底面ABCD是边长为1的菱形,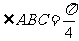 ,
, SA=2,M为SA上的中点,N在线段BC上。
SA=2,M为SA上的中点,N在线段BC上。

(I)当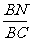 为何值时,MN//平面SCD(说明理由);
为何值时,MN//平面SCD(说明理由);
(II)求MD和平面SCD所成角的正弦值。
16.(本题满分13分)
在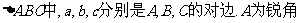 。已知向量
。已知向量
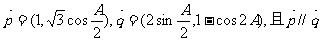 。
。
(I)若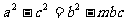 ,求实数m的值;
,求实数m的值;
(II)若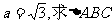 面积的最大值。
面积的最大值。
15.对于集合N={1,2,3,…n},定义其“交替和”如下:按照递减的次序重新排列元素,从最大数开始交替地减、加后继的数,例如集合{2,1,9,6,4}的交替和为9-6+4-2+1=6,集合{5}的交替和为5;当集合n=2时,集合N的所有非空子集为{1},{2},{1,2},则它们的交替和的总和S2=1+2+(2-1)=4。请你尝试当n=3,n=4时,计算它们的所有非空子集的交替和的总和S3,S4,并根据结果猜测集合N={1,2,3,…,n}的所有非空子集的交替的总和Sn为 。
14.设点P、Q、R是线段AB的四等分点,则有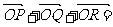
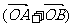
13.若不等式组 表示的平面区域为三角形,则s的取值范围为
。
表示的平面区域为三角形,则s的取值范围为
。
|
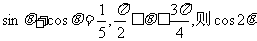 =
。
=
。12.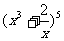 展开式中x3的系数为
。(用数字作答)。
展开式中x3的系数为
。(用数字作答)。
10.将3个相同的黑球和3个相同的白球自左向右排成一排,如果满足:从任何一个位置(含这个位置)开始向左数,黑球的个数总是不小于白球的个数,就称这种排列为“有效排列”,则出现“有效排列”的概率为 ( )
A.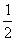 B.
B.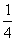 C.
C.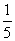 D.
D.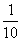
第Ⅱ卷(非选择题 共100分)
9.若点P为共焦点的椭圆C1和双曲线C2的一个交点,F1、F2分别是它们的左右焦点,设椭圆离心率e1,双曲线离心率e2,若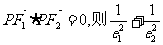 = ( )
= ( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com