
2.若sin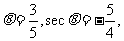 则
则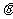 在 ( )
在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.将-3000化为弧度为 ( )
A.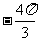 ; B.
; B.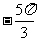 ; C.
; C.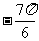 D.
D.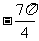
22.(本小题14分)
设实数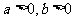 ,且满足
,且满足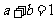
(1)求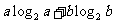 的最小值;
的最小值;
(2)设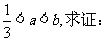 (
(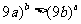
21.(本小题15分)
已知抛物线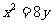 的焦点为
的焦点为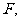
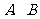 是抛物线上的两动点,且
是抛物线上的两动点,且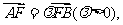 过
过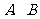 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为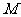
(1)证明线段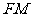 被
被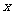 轴平分
轴平分
(2)计算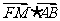 的值
的值
(3)求证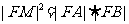
20.(本小题15分)
已知方程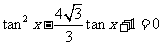 在
在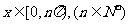 内所有根的和记为
内所有根的和记为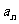
(1)写出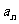 的表达式:(不要求严格的证明)
的表达式:(不要求严格的证明)
(2)求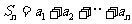 ;
;
(3)设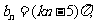 若对任何
若对任何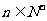 都有
都有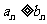 ,求实数
,求实数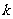 的取值范围。
的取值范围。
19.(本小题14分)
一个多面体的直观图及三视图如下图所示(其中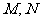 分别是
分别是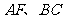 的中点)
的中点)
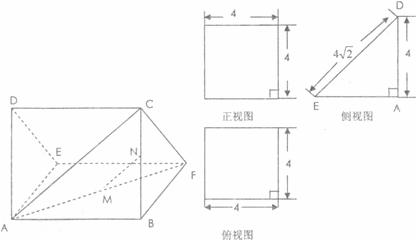
(1)求证: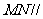 平面
平面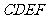 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求多面体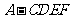 的体积。
的体积。
18.(本小题14分)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选说累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为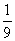 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
(I)求甲选手回答一个问题的正确率;
(Ⅱ)求选手甲可进入决赛的概率;
(Ⅲ)设选手甲在初赛中答题的个数为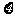 ,试写出
,试写出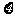 的分布列,并求
的分布列,并求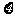 的数学期望。
的数学期望。
17.如果一条直线和一个平面垂直,则称此直线与平面构成一个“正交线面对”,在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成“正交线面对”的概率为____
15.若关于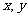 的不等式组
的不等式组 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则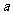 的取值范围是
的取值范围是
_____________
|
 的大小关系为_____
的大小关系为_____14.设双曲线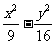 =1的右顶点为
=1的右顶点为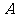 ,右焦点为
,右焦点为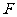 ,过点
,过点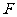 作平行双曲线的一条渐近线的直线与双曲线交于点
作平行双曲线的一条渐近线的直线与双曲线交于点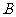 ,则
,则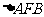 的面积为___________
的面积为___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com