
5.设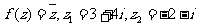 则
则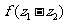 是( )
是( )
A.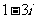 B.
B. C.
C.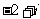 D.
D.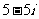
4.上一个n层台阶,若每次可上一层或两层,设所有不同的上法的总数为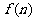 ,则下列猜想中正确的是( )
,则下列猜想中正确的是( )
A.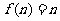 B.
B.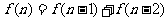
C. D.
D.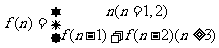
3.某个与正整数有关的命题,能由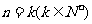 时命题成立推得
时命题成立推得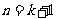 时命题成立,若已知
时命题成立,若已知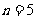 是命题不成立,则以下推理结论正确的是( )
是命题不成立,则以下推理结论正确的是( )
A.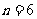 是此命题不成立
B.
是此命题不成立
B.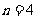 是此命题不成立
是此命题不成立
C.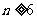 是此命题不成立
D.如果
是此命题不成立
D.如果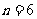 时命题成立,那么对任意
时命题成立,那么对任意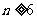 ,此命题成立
,此命题成立
2.已知复数z满足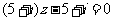 ,则z等于( )
,则z等于( )
A.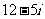 B.
B.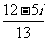 C.
C.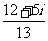 D.
D.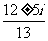
1.复数-9的平方根是 ( )
A.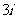 B.
B.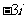 C.
C. D.不存在
D.不存在
20.(本题满分16分)
已知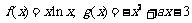 .
.
(1)求函数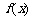 在
在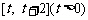 上的最小值;(5分)
上的最小值;(5分)
(2)对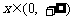 ,不等式
,不等式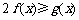 恒成立,求实数a的取值范围;(5分)
恒成立,求实数a的取值范围;(5分)
(3)证明对一切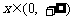 ,都有
,都有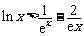 成立.(6分)
成立.(6分)
19.(本题满分16分)设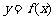 是定义在R上的奇函数, 且当
是定义在R上的奇函数, 且当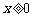 时,
时, 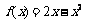 .
.
(1)求当x<0时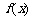 的解析式;(7分)
的解析式;(7分)
(2)问是否存在这样的正数a,b,当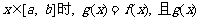 的值域
的值域
为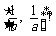 若存在,求出a,b的值,若不存在,请说明理由. (9分)
若存在,求出a,b的值,若不存在,请说明理由. (9分)
18.(本题满分15分)
设函数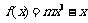 的图象上以
的图象上以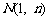 为切点的切线的倾斜角为
为切点的切线的倾斜角为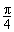 .
.
(1)求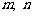 的值;(8分)
的值;(8分)
(2)是否存在最小的正整数 ,使得不等式
,使得不等式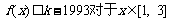 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数 ,若不存在,请说明理由.(7分)
,若不存在,请说明理由.(7分)
17.(本题满分15分)已知集合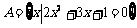 ,
,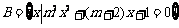 ,若
,若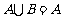 ,求实数m的取值范围.
,求实数m的取值范围.
16.(本题满分14分)为了缓解交通压力,某省在两个城市之间修建一条专用铁路,用一列火车作为公共交通车.如果该列火车每次拖4节车厢,每日能来回16趟;如果每次拖7节车厢,则每日能来回10趟.火车每日每次拖挂车厢的节数是相同的,每日来回趟数y是每次拖挂车厢节数x的一次函数,每节车厢满载时能载客110人.
(1)求出y关于x的函数关系式;(7分)
(2)这列火车满载时每次应拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数. (7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com