
4.“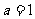 ”是“函数
”是“函数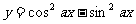 的最小正周期为
的最小正周期为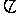 ”的( )条件.
”的( )条件.
A.充分不必要 B.必要不充分
C.充要 D.既不充分条件也不必要.
3.设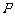 和
和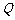 是两个集合,定义集合
是两个集合,定义集合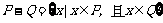 ,如果
,如果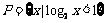 ,
,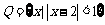 ,那么
,那么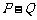 等于 ( )
等于 ( )
A.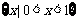 B.
B.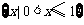 C.
C.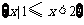 D.
D.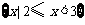
2.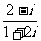 = ( )
= ( )
A.-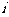 B.i C.1
D.-1
B.i C.1
D.-1
1.与直线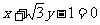 垂直的直线的倾斜角为 ( )
垂直的直线的倾斜角为 ( )
A.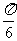 B.
B.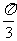 C.
C.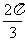 D.
D.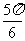
22.(本小题12分)设函数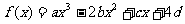 (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时,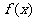 取极小值
取极小值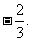
(1)求a、b、c、d的值;
(2)当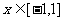 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(3)若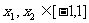 时,求证:
时,求证: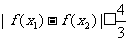 .
.
21.(本小题满分12分)已知抛物线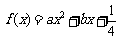 与直线
与直线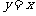 相切于点
相切于点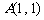 .
.
(1)求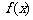 的解析式;
的解析式;
(2)若对任意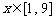 ,不等式
,不等式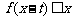 恒成立,求实数
恒成立,求实数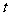 的取值范围.
的取值范围.
20.(本小题12分)已知函数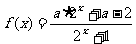 为R上的奇函数
为R上的奇函数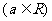 ,求函数f(x)的反函数,并解不等式
,求函数f(x)的反函数,并解不等式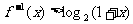
19.(本小题12分)已知函数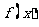 在定义域
在定义域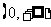 上为增函数,且满足
上为增函数,且满足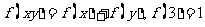
(1)求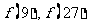 的值
的值
(2)解不等式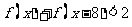
18.(本小题12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验,求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.分别求出该商家检验出不合格产品为1件和2件的概率,并求该商家拒收这批产品的概率.
17.(本小题10分) 设方程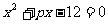 的解集为A,方程
的解集为A,方程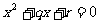 的解集为B,已知
的解集为B,已知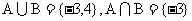 ,试求实数
,试求实数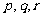 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com