
5.设P为曲线C: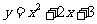 上的点,且曲线C在点P处切线倾斜角的取值范围为
上的点,且曲线C在点P处切线倾斜角的取值范围为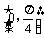 ,则点P横坐标的取值范围为
( )
,则点P横坐标的取值范围为
( )
A.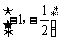 B.
B.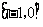 C.
C.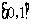 D.
D.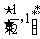
4.函数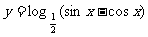 的单调增区间是 ( )
的单调增区间是 ( )
A.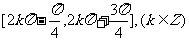 B.
B.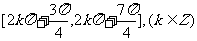
C. 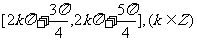 D.
D.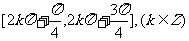
3.若函数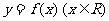 满足
满足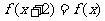 , 且
, 且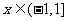 时
时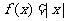 , 则函数
, 则函数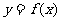 的图象与函数
的图象与函数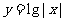 的图象的交点个数为
( )
的图象的交点个数为
( )
A.16 B.18 C.20 D.无数个
2.已知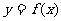 是偶函数,当
是偶函数,当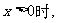
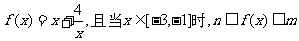 恒成立,则
恒成立,则 的最小值是
( )
的最小值是
( )
A.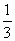 B.
B.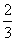 C.1 D.
C.1 D.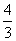
1.设全集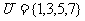 ,集合
,集合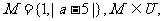 CU M={5,7},则a的值为 ( )
CU M={5,7},则a的值为 ( )
A.2或-8 B.-8或-2 C.-2或8 D.2或8
(17)(本小题满分10分)
在△ABC中,已知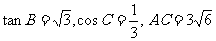
求△ABC的面积.
(18)(本小题满分12分)
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5 (相互独立)
(1)求至少3人同时上网的概率;
(2)至少几人同时上网的概率小于0.3 ?
(19)(本小题满分12分)
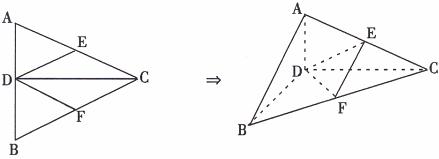
如图所示,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B-AC-D的大小;
(B)求点C到平面DEF的距离.
(20)(本小题满分12分)
已知函数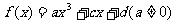 是R上的奇函数,
是R上的奇函数,
当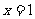 时,
时,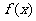 取得极值2.
取得极值2.
(1)求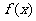 的单调区间:
的单调区间:
(2)若对于任意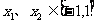 ,不等式
,不等式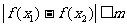 恒成立,求m的最小值.
恒成立,求m的最小值.
(21)(本小题满分12分)
设数列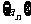 满足
满足
(1)求数列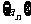 的通项;
的通项;
(2)令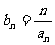 ,求数列
,求数列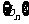 的前n项和
的前n项和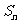 .
.
(22)(本小题满分12分)
设椭圆方程为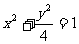 ,过点M(0,1)的直线
,过点M(0,1)的直线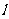 交椭圆于A,B两点,O为坐标原点,点P满足
交椭圆于A,B两点,O为坐标原点,点P满足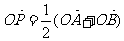 ,点N的坐标为(
,点N的坐标为(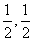 ),当直线
),当直线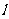 绕点M旋转时,
绕点M旋转时,
求:(1)动点P的轨迹方程;
(2) 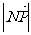 的最大值,最小值.
的最大值,最小值.
(13)某工厂生产A,B,C三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样的方法抽出一个容量为n的样本,样本中A种型号产品有16件,那么此样本的容量n= .
(14)设x,y满足约束条件 ,则
,则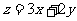 的最大值是
的最大值是
(15)由数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数共有 个.
(16)设F为抛物线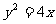 的焦点,A,B,C为该抛物线上三点,若
的焦点,A,B,C为该抛物线上三点,若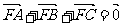 ,则
,则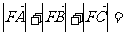
(1)设全集U={一2,一1,0,1,2),A=(一2,一1,0},B=(0,1,2},则(CUA)∩B等于
A.{0} B. {一2,一1} C.{1,2} D.{0,1,2}
(2)曲线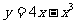 在点(一1,一3)处的切线方程是
在点(一1,一3)处的切线方程是
A.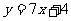 B.
B.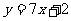 C.
C.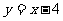 D.
D.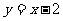
(3)函数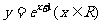 的反函数是
的反函数是
A.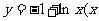 >0) B.
>0) B. >0)
>0)
C. >0) D.
>0) D. >0)
>0)
(4)设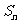 是等差数列
是等差数列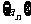 的前n项和,若
的前n项和,若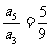 ,则
,则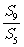 等于
等于
A.2 B.一1 C.1 D.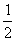
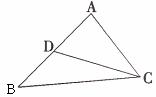
(5)如图所示,D是△ABC的边AB上的中点,则向量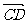 等于
等于
A.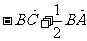 B.
B.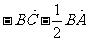
C.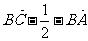 D.
D.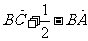
(6) 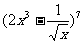 的展开式中常数项是
的展开式中常数项是
A.14 B.一14 C.42 D.一42
(7)设双曲线以椭圆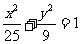 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为
A. B.
B.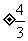 C.
C.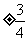 D.
D.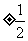
(8)已知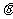 是第三象限角,且
是第三象限角,且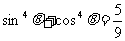 ,那么
,那么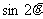 等于
等于
A.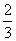 B.
B.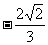 C.
C.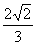 D.
D.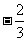
(9)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B,和BB1的中点.那么直线AM与CN所成角的余弦值是
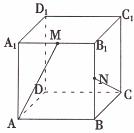
A.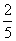 B.
B.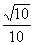 C.
C.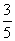 D.
D.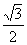
(10) 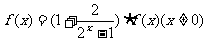 是偶函数,
是偶函数,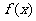 不恒等于零,则
不恒等于零,则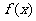
A.是偶函数 B.是奇函数
C.可能是奇函数也可能是偶函数 D.不是奇函数,也不是偶函数
(11)函数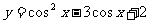 的最小值为
的最小值为
A.2 B.0 C.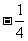 D.6
D.6
(12)球面上有3个点,其中任意两点的球面距离都等于大圆周长的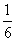 ,经过这三个点的小圆的周长为
,经过这三个点的小圆的周长为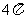 ,那么这个球的半径为
,那么这个球的半径为
A.2
B.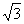 C.4
C.4 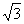 D.2
D.2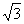
第Ⅱ卷(非选择题 共90分)
(17)(本小题满分10分)
在△ABC中,已知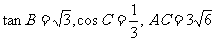
求△ABC的面积.
(18)(本小题满分12分)
在一次购物抽奖活动中,假设某10张券中,有一等奖券1张,可获价值50元的奖品;
有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券
中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值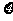 (元)的概率分布列和期望E
(元)的概率分布列和期望E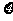 .
.
(19)(本小题满分12分)
如图所示,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC的中点,
现将△ABC沿CD翻折成直二面角A-DC-B.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B-AC-D的大小;
(B)求点C到平面DEF的距离.
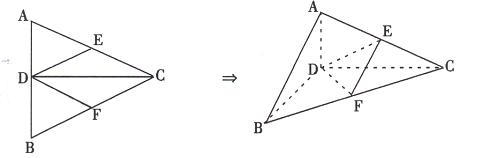
(20)(本小题满分12分)
已知数列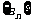 中,
中,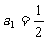 ,点(n,
,点(n,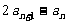 )在直线y=x上,其中n:l,2,3,…
)在直线y=x上,其中n:l,2,3,…
(1)令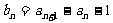 ,求证:数列
,求证:数列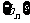 是等比数列;
是等比数列;
(2)求数列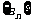 的通项.
的通项.
(21)(本小题满分12分)
设椭圆方程为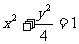 ,过点M(0,1)的直线
,过点M(0,1)的直线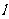 交椭圆于A,B两点,O为坐标原点,
交椭圆于A,B两点,O为坐标原点,
点P满足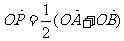 ,点N的坐标为(
,点N的坐标为(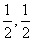 ),当直线
),当直线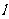 绕点M旋转时,
绕点M旋转时,
求:(1)动点P的轨迹方程;
(2) 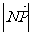 的最大值,最小值.
的最大值,最小值.
(22)(本小题满分12分)
已知函数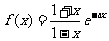
(1)设a>0,讨论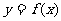 的单调性;
的单调性;
(2)若对任意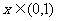 ,恒有
,恒有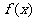 >1,求a的取值范围.
>1,求a的取值范围.
(13)已知直线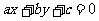 与圆O:
与圆O: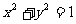 相交于A、B两点,且
相交于A、B两点,且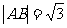 ,
,
则 ·
·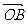 =
.
=
.
(1 4)在某项测量中,测量结果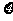 服从正态分布,N(1,
服从正态分布,N(1,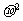 )(
)(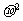 >0).若
>0).若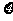 在(0,1)内取
在(0,1)内取
值的概率为0.4,则∈在(0,2)内取值的概率为 .
(15)椭圆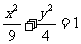 的焦点为F1、F2名P为其上的动点,当∠F1PF2为钝角时,点P
的焦点为F1、F2名P为其上的动点,当∠F1PF2为钝角时,点P
横坐标的取值范围是 。
(16)四个不同的小球放人编号为1、2、3、4的四个盒中,则恰有一个空盒的放法
共有 种(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com