
5.向量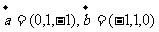 ,则
,则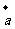 与
与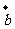 的夹角为
的夹角为
A.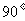 B.
B. 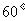 C.
C. 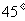 D.
D.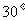
4.双曲线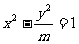 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则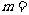 ( )
( )
A.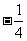 B.
B.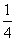 C.
C. D.
D.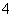
3.抛物线 y2 = 4x 的焦点为F,P为抛物线上一点,P的横坐标为2,则|PF|= ( )
A. 2 B. 3 C. 4 D. 5
2.同时抛掷两枚质地均匀的硬币一次,则出现两个正面朝上的概率是 ( )
A.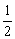 B.
B.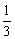 C.
C. 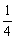 D.
D.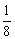
1.下列说法中错误的是 ( )
A.“ $ x∈R, x2+2x+2≤0”的否定是“对"x∈R,x2+2x+2>0”.
B.“p∨q”为真命题,但“p∧q”不一定为真命题.
C.“ab>0”是“a>0且b>0”的充要条件.
D.命题“ 若x2=1,则x=1.”的逆否命题是假命题.
23.甲.乙俩人约定上街购物,他们约定在下午4:00到5:00之间在某一街角相会,他们约好当其中一个先到后一定要等另一个人15分钟。若另一个人仍不到则离去,试问这俩人能够相遇的概率为多大?假定他们到达约定地点的时间是随机的且都在约定的一小时之内。
22.抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2).A(x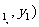 .B(
.B(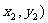 均在抛物线上。
均在抛物线上。
(1)写出抛物线的方程及其准线方程。
(2)当PA与PB的斜率存在且倾斜角互补时,求y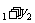 的值及直线AB的斜率
的值及直线AB的斜率
21.已知a为实数,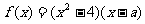
(1)求导数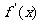
(2)若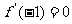 ,求
,求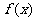 在[-2,2]上的最大值和最小值
在[-2,2]上的最大值和最小值
20.已知双曲线的中心在原点,焦点F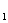 ,F
,F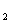 在X轴上,离心率为
在X轴上,离心率为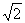
 ,且过点(4,-
,且过点(4,-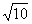 )。
)。
(1)求双曲线方程
(2)若点M(3,m)在双曲线上,求证MF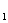 ⊥MF
⊥MF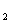
19.某人去开会,他乘火车.轮船.汽车.飞机去的概率分别为0.3,0.2,0.1,0.4
(1)求他乘火车或飞机去的概率
(2)求他不乘轮船去的概率
(3)如果他去的概率为0.5,请问他有可能是乘何种交通工具去的?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com