
9. 从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为 ( )
A.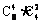 B.
B.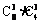 C.
C.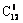 D.
D.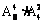
8.已知直线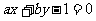 (
(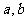 不全为
不全为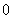 )与圆
)与圆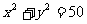 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( )
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( )
A.66条 B.72条 C.74条 D.78条
7.双曲线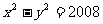 的左、右顶点分别为
的左、右顶点分别为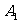 、
、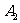 ,
,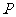 为其右支上一点,且
为其右支上一点,且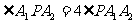 ,则
,则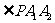 等于
(
)
等于
(
)
A.
无法确定
B.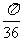 C.
C.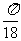 D.
D.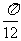
6.若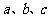 是常数,则“
是常数,则“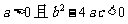 ”是“对任意
”是“对任意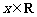 ,有
,有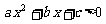 ”的 ( )
”的 ( )
A.充分不必要条件. B.必要不充分条件.
C.充要条件. D.既不充分也不必要条件.
5.设地球的半径为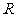 ,若甲地位于北纬
,若甲地位于北纬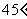 东经
东经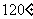 ,乙地位于南纬
,乙地位于南纬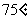 东经
东经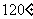 ,则甲、乙两地的球面距离为
(
)
,则甲、乙两地的球面距离为
(
)
A.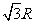 B.
B.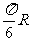 C.
C.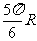 D.
D.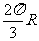
4.已知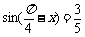 ,则
,则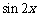 的值为
( )
的值为
( )
A.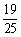 B.
B.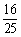 C.
C.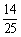 D.
D.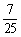
3.在等差数列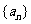 中,若
中,若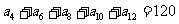 ,则
,则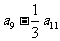 的值为 ( )
的值为 ( )
A.14 B.15 C.16 D.17
2. 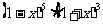 的展开式中
的展开式中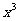 的系数为
( )
的系数为
( )
A.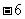 B.
B.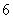 C.
C.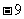 D.
D.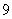
1. 已知映射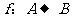 ,其中
,其中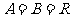 ,对应法则
,对应法则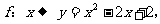 若对实数
若对实数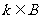 ,在集合A中不存在原象,则
,在集合A中不存在原象,则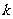 的取值范围是
( )
的取值范围是
( )
A.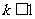 B.
B.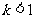 C.
C.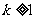 D.
D.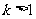
(17)(本小题满分12分)
(理)解关于x的不等式: ,(a>0且a≠1).
,(a>0且a≠1).
(文)解关于x的不等式: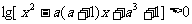 ,(a>0且a≠1).
,(a>0且a≠1).
(18)(本小题满分12分)
已知z1=3+4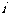 ,z2=65
,z2=65
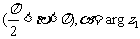 且
且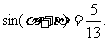
(Ⅰ)求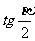 ;
;
(Ⅱ)设z1、z2在复平面内所对应点分别为P、Q、O为坐标原点,以OP、OQ为边作
平行四边形OPRQ,求对角线OR的长及平行四边形OPRQ的面积.
(19)(本小题满分12分)
如图,已知四棱锥P-ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中
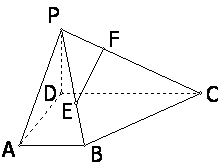 点,F在PC上且PF=
点,F在PC上且PF=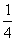 PC.
PC.
(Ⅰ)求证EF//平面PAD;
(Ⅱ)求三棱锥E-PCD的体积.
(20)(本小题满分12分,文科做(Ⅰ)、(Ⅱ),理科全做)
已知奇函数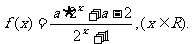
(Ⅰ)试确定实数a的值,并证明f(x)为R上的增函数;
(Ⅱ)记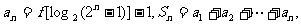 求
求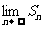 ;
;
(Ⅲ)若方程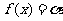 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证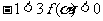 .
.
(21)(本小题满分12分)
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入Tn与时间n(以月为单位)的关系为Tn=an+b,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
(22)(本小题满分14分,文科只做(Ⅰ)、(Ⅱ),理科全做)
已知抛物线C: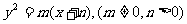 的焦点为原点,C的准线与直线
的焦点为原点,C的准线与直线
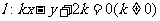 的交点M在x轴上,
的交点M在x轴上,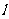 与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
(Ⅰ)求抛物线C的方程;
(Ⅱ)求实数p的取值范围;
(Ⅲ)若C的焦点和准线为椭圆Q的一个焦点和一条准线,试求Q的短轴的端点的轨迹方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com