
1.复数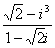 =
=
(A)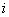 (B)
(B)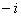
(C)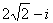 (D)
(D)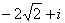
22、(本小题满分14分)
已知函数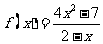 ,
,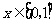
(Ⅰ)求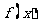 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设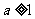 ,函数
,函数 ,
,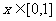 ,若对于任意
,若对于任意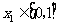 ,总存在
,总存在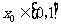 ,使得
,使得 成立,求
成立,求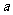 的取值范围
的取值范围
21、(本小题满分12分)
设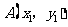 ,
,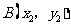 两点在抛物线
两点在抛物线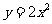 上,
上,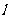 是
是 的垂直平分线。
的垂直平分线。
(Ⅰ)当且仅当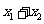 取何值时,直线
取何值时,直线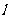 经过抛物线的焦点
经过抛物线的焦点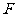 ?证明你的结论;
?证明你的结论;
(Ⅱ)当直线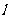 的斜率为2时,求
的斜率为2时,求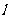 在
在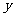 轴上截距的取值范围。
轴上截距的取值范围。
19、(本小题满分12分)
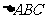 中,内角
中,内角 的对边分别是
的对边分别是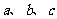 ,已知
,已知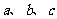 成等比数列,且
成等比数列,且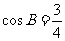
(Ⅰ)求 的值
的值
(Ⅱ)设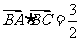 ,求
,求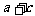 的值。
的值。
20(本小题满分12分)
在等差数列 中,公差
中,公差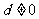 ,
, 是
是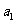 与
与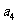 的等比中项,已知数列
的等比中项,已知数列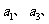

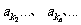 成等比数列,求数列{
成等比数列,求数列{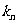 }的通项
}的通项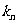
18、(本小题满分12分)
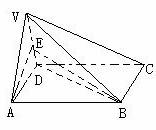
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD
(Ⅰ)证明AB⊥平面VAD;
(Ⅱ)求面VAD与面VDB所成的二面角的大小
17、(本小题满分12分)
设甲、乙、丙三台机器是否需要照顾相互没有影响,已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125
(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别为多少;
(Ⅱ)计算这个小时内至少有一台机器需要照顾的概率
16、已知在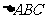 中,
中,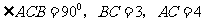 ,
, 是
是 上的点,则点
上的点,则点 到
到 的距离乘积的最大值是
的距离乘积的最大值是
15、设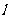 为平面上过点
为平面上过点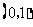 的直线,
的直线,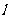 的斜率等可能地取
的斜率等可能地取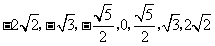 ,用
,用 表示坐标原点到
表示坐标原点到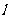 的距离,则随机变量
的距离,则随机变量 的数学期望
的数学期望 。
。
14、已知向量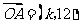 ,
,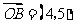 ,
,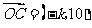 ,且A、B、C三点共线,则
,且A、B、C三点共线,则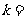 __________
__________
13、已知复数: ,复数
,复数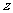 满足
满足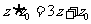 ,则复数
,则复数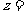
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com