
1.圆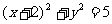 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )
A. B.
B.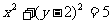
C.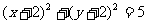 D.
D.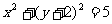
22.(本小题满分12分)
数列{an}满足 .
.
(Ⅰ)用数学归纳法证明: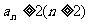 ;
;
(Ⅱ)已知不等式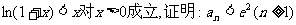 ,其中无理数e=2.71828….
,其中无理数e=2.71828….
21.(本小题满分12分)
已知椭圆C1的方程为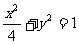 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线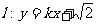 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足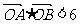 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
20.(本小题满分13分)
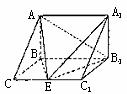
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=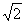 ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=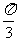 ,求:
,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A-EB1-A1的平面角的正切值.
19.(本小题满分13分)
已知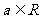 ,讨论函数
,讨论函数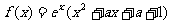 的极值点的个数.
的极值点的个数.
18.(本小题满分13分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值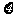 (元)的概率分布列和期望
(元)的概率分布列和期望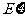 .
.
17.(本小题满分13分)
若函数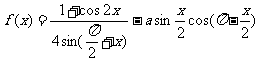 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
16.连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
15.某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
14.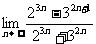 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com