
22.(本题满分14分)
已知函数f(x)在(-1,1)上有定义,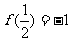 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
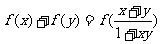 .
.
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列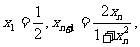 求
求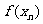 ;
;
(Ⅲ)(理)求证
(文)求证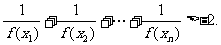
21.(本题满分12分)
 A、B是两个定点,且|AB|=8,动点M到A点的距离
A、B是两个定点,且|AB|=8,动点M到A点的距离
是10,线段MB的垂直平分线l交MA于点P,若以AB
所在直线为x轴,AB的中垂线为y轴建立直角坐标系.
(Ⅰ)试求P点的轨迹c的方程;
(Ⅱ)直线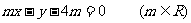 与点P所在
与点P所在
曲线c交于弦EF,当m变化时,试求△AEF的面积的最大值.
19.(文)(本题满分12分)
已知函数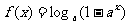 (其中a>0,且a≠1),解关于x的不等式
(其中a>0,且a≠1),解关于x的不等式
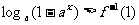
20.(本题满分12分)
一家企业生产某种产品,为了使该产品占有更多的市场份额,拟在2001年度进行一系列的促销活动,经过市场调查和测算,该产品的年销量x万件与年促销费用t万元之间满足:
3-x与t+1(t≥0)成反比例,如果不搞促销活动,该产品的年销量只能是1万件,已知2001年生产该产品的固定投资为3万元,每生产1万件该产品需再投资32万元,当该产品的售价g(x)满足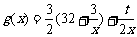 时,则当年的产销量相等.
时,则当年的产销量相等.
(Ⅰ)将2001年的利润y表示为促销费t万元的函数;
(Ⅱ)该企业2001年的促销费投入多少万元时,企业的年利润最大?
(注:利润=收入-生产成本-促销费)
17.(本题满分12分)
设复数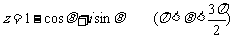 且
且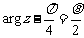 .
.
求 的值.
的值.
18.(理)(本题满分共12分)
 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为
棱A1C1上的动点.
(Ⅰ)当M在何处时,BC1//平面MB1A,并证明之;
(Ⅱ)在(I)下,求平面MB1A与平面ABC所成的二
面角的大小;
(Ⅲ)求B-AB1M体积的最大值.
18.(文)(图同理18,本题满分12分)
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为
棱A1C1的中点
(Ⅰ)求证BC1//平面MB1A;
(Ⅱ)求平面MB1A与平面ABC所成的二面角的正切值;
(Ⅲ)求B-AMB1的体积.
19.(理)(本题满分12分)
设常数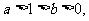 不等式
不等式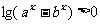 的解集为M
的解集为M
(Ⅰ)当ab=1时,求解集M;
(Ⅱ)当M=(1,+∞)时,求出a,b应满足的关系.
18.(本小题满分12分)
(文科做)甲、乙两人在罚球线投球命中的概率分别为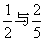 .
.
(Ⅰ)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率.
(理科做)甲、乙两人在罚球线投球命中的概率分别为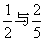 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(Ⅰ)甲、乙两人在罚球线各投球一次,求两人得分之和ξ的数学期望;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率;
19(本小题满分12分).
[文科做(1)、(2)小题,理科做(1)、(3)小题]
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
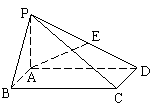 (1)求证:平面PDC⊥平面PAD;
(1)求证:平面PDC⊥平面PAD;
(2)若E是PD的中点,求异面直线AE
与PC所成角的余弦值;
(3)在BC边上是否存在一点G,使得D点
到平面PAG的距离为1,若存在,求出BG的值;若不存在,请说明理由.
20.(本小题满分12分)
已知直线L:y=-x+1与 椭圆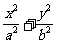 =1(a>b>0)相交于A、B两点,且线段AB的中点为(
=1(a>b>0)相交于A、B两点,且线段AB的中点为(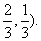
(1)求此椭圆的离心率;
(2)若椭圆的右焦点关于直线L的对称点在圆x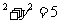 上,求此椭圆的方程.
上,求此椭圆的方程.
21.(本小题满分12分).
设数列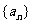 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,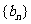 为等比数列,且
为等比数列,且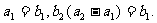
(Ⅰ)求数列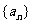 和
和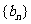 的通项公式;
的通项公式;
(Ⅱ)设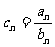 ,求数列
,求数列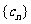 的前n项和Tn.
的前n项和Tn.
22.(本小题满分14分).
函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,Q(x-2a,-y)是函数y=g(x)图象上的点.
(1)写出函数y=g(x)的解析式;
(2)当x=1,a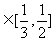 时,求H(a)=g -1(x)的值域;
时,求H(a)=g -1(x)的值域;
(3)当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
17.(本小题满分12分)
已知向量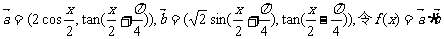 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
16. P是双曲线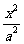 -
-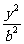 =1(a>0,b>0)的左支上一点,F1、F2分别为左、右焦点,且焦距为2c,则△PF1F2的内切圆的圆心横坐标为_________.
=1(a>0,b>0)的左支上一点,F1、F2分别为左、右焦点,且焦距为2c,则△PF1F2的内切圆的圆心横坐标为_________.
15.用火柴棒按下图的方法搭三角形:

按图示的规律搭下去,则所用火柴棒数an 与所搭三角形的个数n之间的关系式可以是
14.在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式。如从指数函数中可抽象出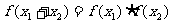 的性质;从对数函数中可抽象出
的性质;从对数函数中可抽象出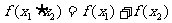 的性质。那么从函数
(写出一个具体函数即可)可抽象出
的性质。那么从函数
(写出一个具体函数即可)可抽象出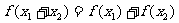 的性质。
的性质。
13.(文科做)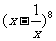 的展开式中,常数项为 。(用数字作答)
的展开式中,常数项为 。(用数字作答)
(理科做)若x>-1,则函数f(x)=x+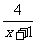 的最小值是_______________.
的最小值是_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com