
(17)(本小题满分12分)
已知函数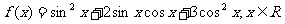 求:
求:
(Ⅰ)求函数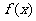 的最大值及取得最大值的自变量x的集合;
的最大值及取得最大值的自变量x的集合;
(Ⅱ)函数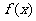 的单调增区间.
的单调增区间.
(18)(本小题满分12分)
甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响.求:
(Ⅰ)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(Ⅱ)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
(19)(本小题满分12分)
已知正方形ABCD,E、F分别是边AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为
(Ⅰ)证明BF∥平面ADE;
(Ⅱ)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角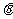 的余弦值.
的余弦值.
(20)(本小题满分12分)
已知等差数列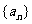 的前n项和为
的前n项和为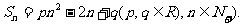
(Ⅰ)求q的值;
(Ⅱ)若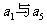 的等差中项为18,
的等差中项为18,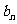 满足
满足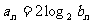 ,求数列{
,求数列{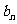 }的前n项和.
}的前n项和.
(21)(本小题满分12分)
已知函数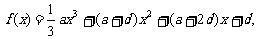
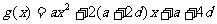 ,其中
,其中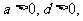 设
设 为
为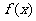 的极小值点,
的极小值点,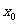 为
为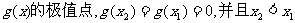 .
.
将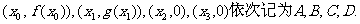
(Ⅰ)求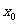 的值;
的值;
(Ⅱ)若四边形ABCD为梯形,且面积为1,求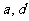 的值.
的值.
(22)(本小题满分14分)
已知点 是抛物线
是抛物线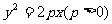 上的两个动点,O是坐标原点,向量
上的两个动点,O是坐标原点,向量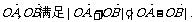 设圆C的方程为
设圆C的方程为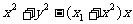
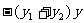
(Ⅰ)证明线段AB是圆C的直径;
(Ⅱ)当圆C的圆心到直线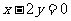 的距离的最小值为
的距离的最小值为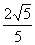 时,求
时,求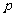 的值.
的值.
(13)方程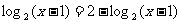 的解为
.
的解为
.
 (14)设
(14)设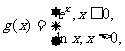 则
则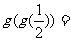 .
.
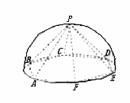
(15)如图,半径为2的半球内有一内接正六棱锥P-ABCDEF,
则此正六棱锥的侧面积是 .
(16)5名乒乓球队员中,有2名老队员和3名新队员,现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员,且1、2号中至少有1名新队员的排法有
种.(以数作答)
(1)函数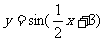 的最小正周期是
的最小正周期是
(A)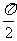 (B)
(B)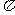 (C)2
(C)2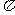 (D)4
(D)4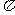
(2)设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是
(A)1 (B)3 (C)4 (D)8
(3)设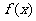 是R上的任意函数,则下列叙述正确的是
是R上的任意函数,则下列叙述正确的是
(A)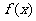
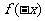 是奇函数
(B)
是奇函数
(B)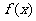 |
|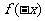 | 是奇函数
| 是奇函数
(C)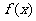 -
-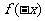 是偶函数 (D)
是偶函数 (D)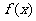 +
+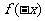 是偶函数
是偶函数
(4)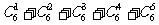 的值为
的值为
(A)61 (B)62 (C)63 (D)64
(5)方程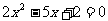 的两个根可分别作为
的两个根可分别作为
(A)一椭圆和一双曲线的离心率 (B)两抛物线的离心率
(C)一椭圆和一抛物线的离心率 (D)两椭圆的离心率
(6)给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线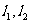 与同一平面所成的角相等,则
与同一平面所成的角相等,则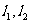 互相平行.
互相平行.
④若直线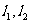 是异面直线,则与
是异面直线,则与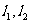 都相交的两条直线是异面直线.
都相交的两条直线是异面直线.
其中假命题的个数是
(A)1 (B)2 (C)3 (D)4
(7)双曲线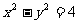 的两条渐近线与直线
的两条渐近线与直线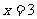 围成一个三角形区域,表示该区域的不等式
围成一个三角形区域,表示该区域的不等式
组是
(A) (B)
(B) (C)
(C) (D)
(D)
(8)设+是R上的一个运算,A是R的非空子集.
若对任意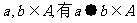 ,则称A对运
,则称A对运
算+封闭. 下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是
(A)自然数集 (B)整数集 (C)有理数集 (D)无理数集
(9)△ABC的三内角A,B,C,所对边的长分别为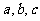 ,设向量p
,设向量p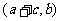 、q=
、q=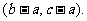
若p∥q,,则角C的大小为
(A)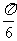 (B)
(B)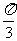 (C)
(C)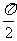 (D)
(D)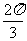
(10)已知等腰△ABC的腰为底的2倍,顶角的正切值是
(A)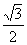 (B)
(B)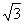 (C)
(C)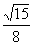 (D)
(D)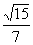
(11)与方程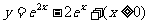 的曲线关于直线
的曲线关于直线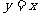 对称的曲线的方程为
对称的曲线的方程为
(A)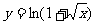 (B)
(B)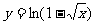
(C)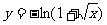 (D)
(D)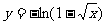
(12)曲线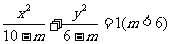 与曲线
与曲线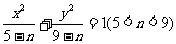 的
的
(A)离心率相等 (B)焦距相等 (C)焦点相同 (D)准线相同
绝密★启用前
2006年普通高等学校招生全国统一考试(辽宁卷)
数学(供文科考生使用)
第II卷(非选择题 共90分)
(17)(本小题满分12分)
已知函数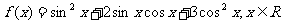 求:
求:
(Ⅰ)求函数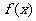 的最大值及取得最大值的自变量x的集合;
的最大值及取得最大值的自变量x的集合;
(Ⅱ)函数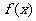 的单调增区间.
的单调增区间.
(18)(本小题满分12分)
已知正方形ABCD,E、F分别是边AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为
(Ⅰ)证明BF∥平面ADE;
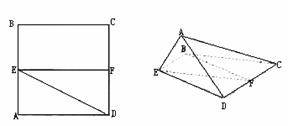 (Ⅱ)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角
(Ⅱ)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角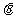 的余弦值.
的余弦值.
(19)(本小题满分12分)
现有甲、乙两个项目,对甲项目每投资十万元,一年后剩是1.2万元、1.18万元、1.17万元的概率分别为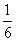 、
、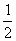 、
、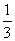 ;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是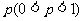 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为ξ对乙项目每投资十万元,ξ取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元. 随机变量ξ1,ξ2分别表示对甲、乙两项目各投资十万元一年后的利润.
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为ξ对乙项目每投资十万元,ξ取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元. 随机变量ξ1,ξ2分别表示对甲、乙两项目各投资十万元一年后的利润.
(Ⅰ)求ξ1,ξ2的概率分布和数学期望Eξ1,Eξ2;
(Ⅱ)当Eξ1<Eξ2时,求p的取值范围.
(20)(本小题满分14分)
已知点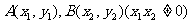 是抛物线
是抛物线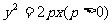 上的两个动点,O是坐标原点,向量
上的两个动点,O是坐标原点,向量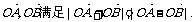 设圆C的方程为
设圆C的方程为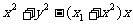
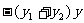
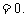
(Ⅰ)证明线段AB是圆C的直径;
(Ⅱ)当圆C的圆心到直线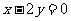 的距离的最小值为
的距离的最小值为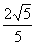 时,求
时,求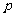 的值.
的值.
(21)(本小题满分12分)
已知函数
设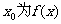 的极小值点. 在[
的极小值点. 在[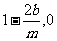 ]上,
]上,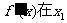 处取得最大值,在
处取得最大值,在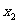 取得最小值. 将
取得最小值. 将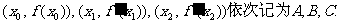
(Ⅰ)求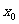 的值;
的值;
(Ⅱ)若△ABC有一条边平行于x轴,且面积为2+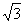 ,求
,求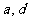 的值.
的值.
(22)(本小题满分2分)
已知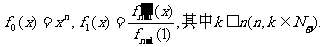 设
设
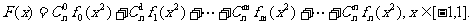
(Ⅰ)写出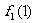 ;
;
(Ⅱ)证明:对任意的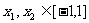 ,情有|
,情有|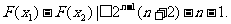
(13)设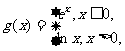 则
则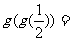 .
.
(14)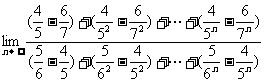 =
.
=
.
(15)5名乒乓球队员中,有2名老队员和3名新队员,现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员,且1、2号中至少有1名新队员的排法有
种.(以数作答)
(16)若一条直线与一个正四棱柱各个面所成的角都为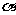 ,则cos
,则cos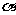 =
.
=
.
(1)设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是
(A)1 (B)3 (C)4 (D)8
(2)设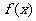 是R上的任意函数,则下列叙述正确的是
是R上的任意函数,则下列叙述正确的是
(A)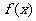
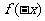 是奇函数
(B)
是奇函数
(B)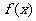 |
|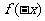 | 是奇函数
| 是奇函数
(C)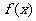 -
-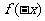 是偶函数 (D)
是偶函数 (D)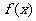 +
+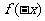 是偶函数
是偶函数
(3)给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线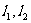 与同一平面所成的角相等,则
与同一平面所成的角相等,则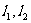 互相平行.
互相平行.
④若直线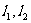 是异面直线,则与
是异面直线,则与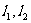 都相交的两条直线是异面直线.
都相交的两条直线是异面直线.
其中假命题的个数是
(A)1 (B)2 (C)3 (D)4
(4)双曲线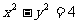 的两条渐近线与直线
的两条渐近线与直线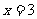 围成一个三角形区域,表示该区域的不等式
围成一个三角形区域,表示该区域的不等式
组是
(A) (B)
(B) (C)
(C) (D)
(D)
(5)设+是R上的一个运算,A是R的非空子集.
若对任意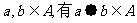 ,则称A对运
,则称A对运
算+封闭. 下列数集对加法、减法、乘法和法(除数不等于零)四则运算都封闭的是
(A)自然数集 (B)整数集 (C)有理数集 (D)无理数集
(6)△ABC的三内角A,B,C,所对边的长分别为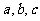 ,设向量p
,设向量p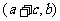 、q=
、q=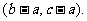
若p∥q,,则角C的大小为
(A)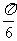 (B)
(B)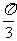 (C)
(C)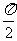 (D)
(D)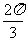
(7)与方程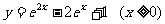 的曲线关于直线
的曲线关于直线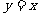 对称的曲线的方程为
对称的曲线的方程为
(A)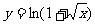 (B)
(B)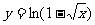
(C)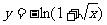 (D)
(D)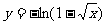
(8)曲线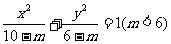 与曲线
与曲线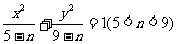 的
的
(A)焦距相等 (B)离心率相等 (C)焦点相同 (D)准线相同
(9)在等比数列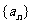 中,
中,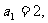 前n项和为
前n项和为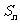 ,若数列
,若数列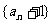 也是等比数列,则
也是等比数列,则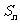 等于
等于
(A)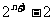 (B)3n (C)2n (D)
(B)3n (C)2n (D)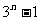
(10)直线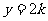 与曲线
与曲线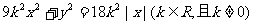 的公共点的个数为
的公共点的个数为
(A)1 (B)2 (C)3 (D)4
(11)已知函数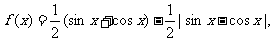 则
则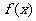 的值域是
的值域是
(A)[-1,1] (B)[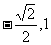 ] (C)
] (C)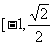 ] (D)
] (D)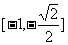
(12)设O(0,0),A(1,0),B(0,1),点P是线段AB上的一个动点,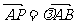 .
.
若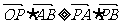 ,则实数
,则实数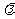 的取值范围是
的取值范围是
(A)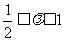 (B)
(B)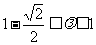
(C)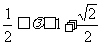 (D)
(D)
绝密★启用前
2006年普通高等学校招生全国统一考试(辽宁卷)
数学(供理科考生使用)
第II卷(非选择题 共90分)
22.(本小题满分14分)
已知各项均为正数的数列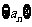 ,满足:
,满足: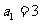 ,且
,且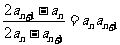 ,
,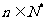 .
.
(1)求数列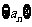 的通项公式;
的通项公式;
(2)设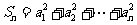 ,
,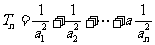 ,求
,求 ,并确定最小正整数
,并确定最小正整数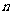 ,使
,使 为整数.
为整数.
21.(本小题满分12分)
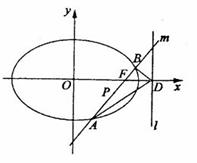
如图,椭圆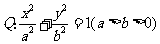 的右焦点为
的右焦点为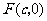 ,过点
,过点 的一动直线
的一动直线 绕点
绕点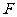 转动,并且交椭圆于
转动,并且交椭圆于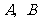 两点,
两点,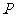 为线段
为线段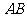 的中点.
的中点.
(1)求点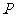 的轨迹
的轨迹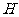 的方程;
的方程;
(2)若在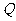 的方程中,令
的方程中,令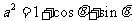 ,
,
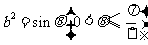 .
.
设轨迹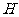 的最高点和最低点分别为
的最高点和最低点分别为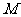 和
和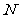 .当
.当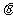 为何值时,
为何值时,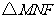 为一个正三角形?
为一个正三角形?
20.(本小题满分12分)
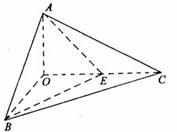
如图,已知三棱锥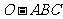 的侧棱
的侧棱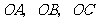 两两垂直,且
两两垂直,且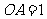 ,
,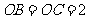 ,
,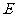 是
是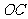 的中点.
的中点.
(1)求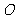 点到面
点到面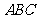 的距离;
的距离;
(2)求异面直线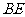 与
与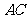 所成的角;
所成的角;
(3)求二面角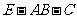 的大小.
的大小.
19.(本小题满分12分)
在锐角 中,角
中,角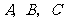 所对的边分别为
所对的边分别为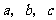 ,已知
,已知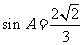 ,
,
(1)求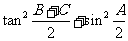 的值;
的值;
(2)若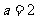 ,
,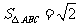 ,求
,求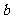 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com