
1.(文科做)sin600° = ( )
(A) –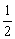 (B)–
(B)–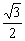 . (C)
. (C)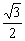 . (D)
. (D) 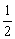 .
.
(理科做)设z = 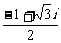 , 则z2 等于( )
, 则z2 等于( )
(A) 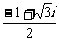 . (B)
. (B) 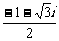 . (C)
. (C) 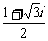 . (D)
. (D) 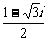 .
.
22.(文)已知数列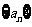 满足
满足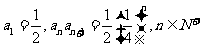 .(1)求数列
.(1)求数列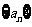 的通项公式;(2)若数列
的通项公式;(2)若数列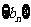 的前n项和
的前n项和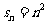 ,
,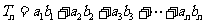 ,求证:
,求证: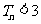 。
。
22.(本小题满分14分)
已知数列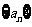 满足
满足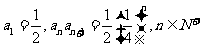 .(1)求数列
.(1)求数列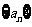 的通项公式;(2)设a>0,数列
的通项公式;(2)设a>0,数列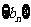 满足
满足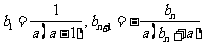 ,若
,若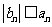 对
对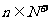 成立,试求a的取值范围。
成立,试求a的取值范围。
21.(本小题满分12分)
已知抛物线C的顶点在原点,以双曲线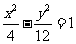 的左准线为准线,(1)求抛物线C的方程;(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP、AQ,且AP⊥AQ,是否存在常数h,使得
的左准线为准线,(1)求抛物线C的方程;(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP、AQ,且AP⊥AQ,是否存在常数h,使得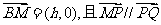 ?
?
20.(本小题满分12分)
(理)已知a>1,函数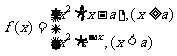 ,求函数f(x)在
,求函数f(x)在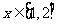 时的最小值。
时的最小值。
(文)已知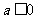 ,求函数
,求函数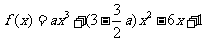 的单调区间。
的单调区间。
19. (本小题满分12分)
(本小题满分12分)
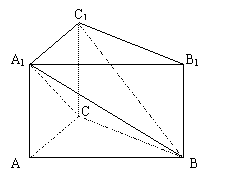
已知直三棱柱ABC-A1B1C1中,AB= 4,AC=AA1=2,∠CAB=60°。
(1) 求证:A1C⊥B1C1;
(2) 求点B1到平面A1BC的距离;
(3) 求二面角C1-A1B-C的大小。
18. (本小题满分12分)
某人抛掷一枚硬币,出现正反的概率都是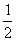 ,构造数列
,构造数列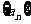 ,使得
,使得 ,记
,记 。
。
(1) 求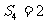 的概率;
的概率;
(2) 求:前两次均出现正面,且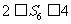 的概率。
的概率。
(3) (理科做文科不做)记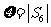 ,求
,求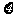 的数学期望。
的数学期望。
17.(本小题满分12分)
已知: (
(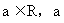 为常数)
为常数)
(I)若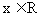 ,求
,求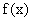 的最小正周期;
的最小正周期;
(II)若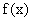 在
在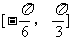 上最大值与最小值之和为3,求a的值。
上最大值与最小值之和为3,求a的值。
16.将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥的侧面和底面分别叫为直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.请仿照直角三角形以下性质:(1)斜边的中线长等于斜边边长的一半;(2)两条直角边边长的平方和等于斜边边长的平方;(3)斜边与两条直角边所成角的余弦平方和等于1.写出直角三棱锥相应性质(至少一条): .
15.已知变量x、y满足 ,若使z=x+ky最小的最优解有无穷多个,则k的值是_____。
,若使z=x+ky最小的最优解有无穷多个,则k的值是_____。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com