
5.设直接过点(0,a),其斜率为1,且与圆x2+y2 =2相切,则a的值为
(A)±4 (B) ±2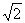 (C) ±2 (D)
±
(C) ±2 (D)
±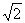
4.设函数f(x)= 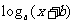 (a>0,a≠1)的图像过点(0,0),其反函数的图像过点(1,2),则
(a>0,a≠1)的图像过点(0,0),其反函数的图像过点(1,2),则 等于
等于
(A)3 (B)4 (C)5 (D)6
3.已知等差数列{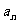 }中,a2+ a3
=8,则该数列前9项和
}中,a2+ a3
=8,则该数列前9项和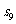 等于
等于
(A)45 (B)36 (C)27 (D)18
2.函数f(x)= 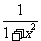 (x
(x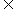 R)的值域是
R)的值域是
(A)[0,1] (B)[0,1) (C)(0,1] (D)(0,1]
1.已知集合P={x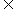
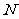
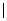 1≤x≤10},集合Q={x
1≤x≤10},集合Q={x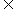 R|x2
+x-6=0.则P
R|x2
+x-6=0.则P 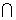 Q等于
Q等于
(A){-2,3} (B){-3,2} (C){3} (D){2}
(17)(本小题满分12分)
已知函数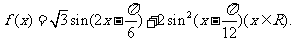
(I)求函数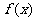 的最小正周期;
的最小正周期;
(II)求使函数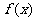 取得最大值的
取得最大值的 集合。
集合。
(18)(本小题满分12分)
甲、乙、丙3人投篮,投进的概率分别是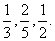
(I)现3人各投篮1次,求3人都没有投进的概率;
(II)用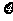 表示投篮3次的进球数,求随机变量
表示投篮3次的进球数,求随机变量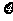 的概率分布及数学期望
的概率分布及数学期望
(19)(本小题满分12分)
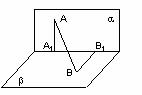
如图,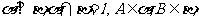 点A在直线
点A在直线 上的射影为
上的射影为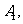 点B在
点B在 上的射影为
上的射影为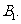 已知
已知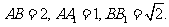 求:
求:
(I)直线AB分别与平面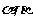 所成角的大小;
所成角的大小;
(II)二面角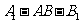 的大小。
的大小。
(20)(本小题12分)
已知正项数列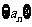 ,其前
,其前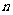 项和
项和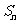 满足
满足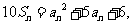 且
且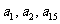 成等比数列,求数列
成等比数列,求数列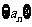 的通项
的通项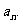
(21)(本小题满分为12分)
如图,三定点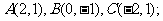 三动点D、E、M满足
三动点D、E、M满足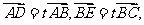
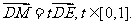

(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
(22)(本小题满分14分)
已知函数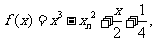 且存在
且存在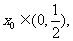 使
使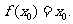
(I)证明: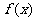 是R上的单调增函数;
是R上的单调增函数;
设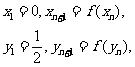 其中
其中 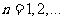
(II)证明: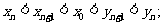
(III)证明: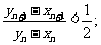
16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有_____种(用数字作答)。
15.水平桌面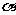 上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形)。在这4个球的上面放一个半径为R的小球,它和下面的4个球恰好相切,则小球的球心到水平桌面
上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形)。在这4个球的上面放一个半径为R的小球,它和下面的4个球恰好相切,则小球的球心到水平桌面 的距离是____。
的距离是____。
14.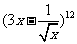 展开式中
展开式中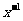 的常数项为_____(用数字作答)。
的常数项为_____(用数字作答)。
13. 的值为______。
的值为______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com