
19. (本小题满分12分,第一、第二小问满分各6分)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为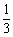 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求至少两次实验成功的概率;
(2) 第二小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.
18.(本小题满分12分,第一、第二小问满分各6分)某港口水的深度 y(米)是时间t(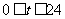 ,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
13.0 |
10.01 |
7.0 |
10.0 |
经长期观察,y=f(t)的曲线可以近似地看成函数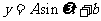 的图象.
的图象.
(Ⅰ)试根据以上数据,求出函数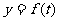 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需的时间).
17. (本小题满分12分,第一、第二、第三小问满分各4分)
已知函数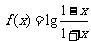 .
.
(1)求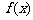 的定义域;
的定义域;
(2)求该函数的反函数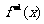 ;
;
(3)判断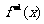 的奇偶性.
的奇偶性.
16.如果直线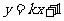 与圆
与圆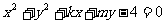 相交于
相交于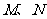 两点,且点
两点,且点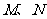 关于直线
关于直线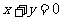 对称,则不等式组
对称,则不等式组 所表示的平面区域的面积为________.
所表示的平面区域的面积为________.
15.定义一种运算“ ”对于正整数满足以下运算性质:
”对于正整数满足以下运算性质:
(1)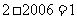 ;(2)
;(2)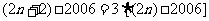 ,则
,则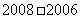 的值是
的值是
14.函数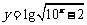 的定义域是
.
的定义域是
.
13.命题“若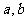 都是偶数,则
都是偶数,则 是偶数”的否命题是_________
是偶数”的否命题是_________
12.半径为4的球面上有A、B、C、D四点,且AB,AC,AD两两互相垂直,则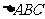 、
、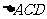 、
、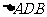 面积之和
面积之和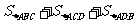 的最大值为 ( )
的最大值为 ( )
A.8 B.16 C.32 D.64
第Ⅱ卷(非选择题 共90分)
11.用正偶数按下表排列
|
|
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
|
第一行 |
|
2 |
4 |
6 |
8 |
|
第二行 |
16 |
14 |
12 |
10 |
|
|
第三行 |
|
18 |
20 |
22 |
24 |
|
… |
|
… |
28 |
26 |
|
则2006在第 行第 列.
A.第 251 行第 3 列 B.第 250 行第 4 列
C.第 250 行第 3 列 D.第 251 行第 4 列
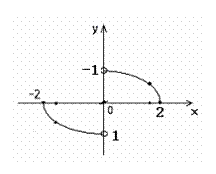
10.如图,函数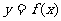 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在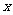 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式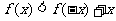 的解集为 ( )
的解集为 ( )
 A.
A.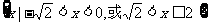
B.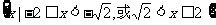
C.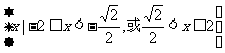
D.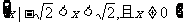
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com