
19.(本小题满分12分)
设二次函数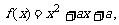 方程
方程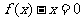 的两根
的两根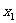 和
和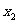 满足
满足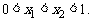
(Ⅰ)求实数a的取值范围;
(Ⅱ)试比较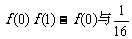 的大小,并说明理由.
的大小,并说明理由.
18.(本小题满分12分)
某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格。销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x(单位:元,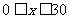 )的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
(Ⅰ)将一个星期的商品销售利润表示成x的函数;
(Ⅱ)如何定价才能使一个星期的商品销售利润最大?
17.(本小题满分12分)
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC;D是AB的中点,且AC=BC=a,∠VDC=θ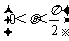 .
.
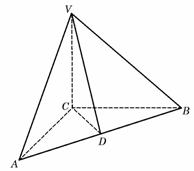
(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)试确定角θ的值,使得直线BC与平面VAB所成的角为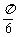 .
.
16.(本小题满分12分)
已知函数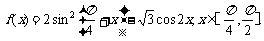
(Ⅰ)求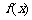 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若不等式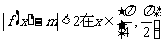 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
15.为了预防流感,某学校对教室用药物消毒法进行消毒。已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为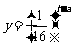 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
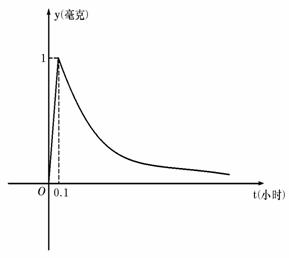
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 ;
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过 小时后,学生才能回到教室。
14.某篮球运动员在三分线投球的命中率是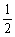 ,他投球10次,恰好投进3个球的概率为 .
,他投球10次,恰好投进3个球的概率为 .
(用数值作答)
13.已知函数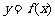 的图象在M(1,f(l))处的切线方程是
的图象在M(1,f(l))处的切线方程是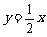 +2,
+2,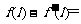
12.过双曲线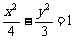 左焦点F1的直线交双曲线的左焦点M、N两点,F2为其右焦点,则|MF2|+|NF2|-|MN|的值为
。
左焦点F1的直线交双曲线的左焦点M、N两点,F2为其右焦点,则|MF2|+|NF2|-|MN|的值为
。
11.设变量x, y满足约末条件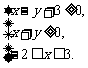 则目标函数2x+y的最小值为____________.
则目标函数2x+y的最小值为____________.
10.已知p是r的充分条件而不是必要条件,q是r的充分条件,s是r的必要条件,q是s的必要条件,现有下列命题:
①s是q的充要条件;
②p是q的充分条件而不是必要条件;
③r是q的必要条件而不是充分条件;
④┐p是┑s的必要条件而不是充分条件;
⑤r是s的充分条件而不是必要条件.
则正确命题的序号是
A.①④⑤ B.①②④ C.②③⑤ D.②④⑤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com