
6.复数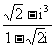 等于
等于
(A)i (B)-i (C)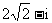 (D)
(D)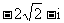
5.如图是一个空间几何体的主视图(正视图)、侧视图、俯视图,直角三角形的直角边长均为1,则这个几何体的体积为
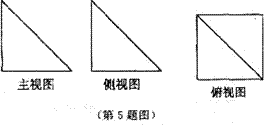
(A)1 (B)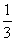 (C)
(C)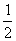 (D)
(D)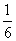
4.某地的财政收入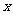 与财政支出
与财政支出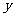 满足线性回归模型
满足线性回归模型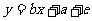 (单位:亿元),其中
(单位:亿元),其中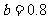 ,
,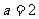 ,
,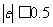 如果今年该地区财政收入为10亿元,则年财政支出预计不会超过
如果今年该地区财政收入为10亿元,则年财政支出预计不会超过
(A)10亿元 (B)9亿元 (C)10.5亿元 (D)9.5亿元
3.给出下列四个命题,其中正确的一个是
(A)在线性回归模型中,相关指数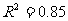 ,说明预报变量对解释变量的贡献率是85%
,说明预报变量对解释变量的贡献率是85%
(B)随机误差e是衡量预报精确度的一个量,它满足E(e)=0
(C)在独立性检验时,两个变量的2×2列联表中对角线上数据的乘积相差越大,说明这两个变量没有关系成立的可能性就越大
(D)相关指数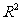 用来刻画回归效果,
用来刻画回归效果,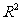 越小,则残差平方和越大,模型的拟合效果越好
越小,则残差平方和越大,模型的拟合效果越好
2.演绎推理“因为对数函数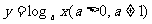 是增函数,而函数
是增函数,而函数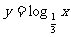 是对数函数,所以
是对数函数,所以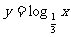 是增函数。所得结论错误的原因是
是增函数。所得结论错误的原因是
(A)大前提错误 (B)小前提错误
(C)推理形式错误 (D)大前提和小前提都错误
1.用C、R和I分别表示复数集、实数集和纯虚数集,其中全集U=C,那么有
(A)C=R∪I (B)R∩I={0} (C)C∪R=C∩I (D)R∩I=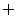
21.(本小题满分12分)
已知函数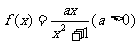
(1)求函数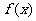 的单调区间;
的单调区间;
(2)当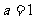 时,求函数
时,求函数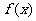 在
在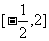 上的最小值;
上的最小值;
(3)当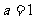 时,求证直线
时,求证直线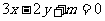 不可能是曲线
不可能是曲线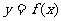 的切线。
的切线。
20.(本小题满分l2分)
已知数列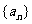 的通项公式为
的通项公式为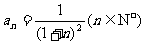 ,记
,记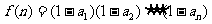 。
。
(1)试求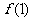 ,
,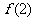 ,
,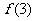 的值;
的值;
(2)猜想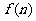 的值,并用数学归纳法证明你的猜想。
的值,并用数学归纳法证明你的猜想。
19.(本小题满分12分)
某单位有8名员工,其中有5名员工曾经参加过一种或几种技能培训,另外3名员工没有参加过任何技能培训,现要从8名员工中任选3人参加一种新的技能培训。
(1)求恰好选到1名曾经参加过技能培训的员工的概率;
(2)这次培训结束后,仍然没有参加过任何技能培训的员工人数ξ是一个随机变量,求ξ的分布列和数学期望。
18.(本小题满分10分)
已知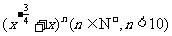 的展开式中第5项,第6项,第7项的系数成等差数列,求展开式中
的展开式中第5项,第6项,第7项的系数成等差数列,求展开式中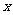 的指数为整数的项。
的指数为整数的项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com