
18.(本小题满分13分)
(理科学生做)
已知函数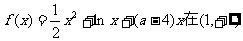 上是增函数.
上是增函数.
(I)求实数a的取值范围;
(II)在(I)的结论下,设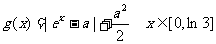 ,求函数
,求函数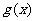 的最小值.
的最小值.
(文科学生做)
已知函数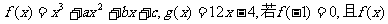 的图象在点
的图象在点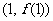 处的切线方程为
处的切线方程为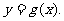
(I)求实数a,b,c的值;
(II)求函数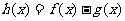 的单调区间.
的单调区间.
17.(本小题满分13分)
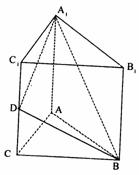
如图,直三棱柱ABC-A1B1C1中,C1C=CB=CA=2,AC⊥CB,D是棱的中点.
(I)求点B到平面A1C1CA的距离;
(II)求二面角B-A1D-A的大小.
16.(本小题满分13分)
口袋里有4个黑球和2个红球共6个球,某人每天从口袋里取球两次,每次任意取一个球,用完后将球放回口袋内才能再次取球.
(I)求这个人在一天中所取的球为同色的概率;
(II)求这个人在连续四天中恰有两天每天所取的球为不同色的概率.
15.(本小题共13分)
在△ABC中,角A、B、C的对边分别为a、b、c,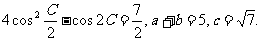
(I)求角C的大小;
(II)求△ABC的面积.
14.动点P在抛物线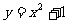 上运动,则动点P和两定点A(-1,0)、B(0,-1)所成的△PAB的重心的轨迹方程是
.
上运动,则动点P和两定点A(-1,0)、B(0,-1)所成的△PAB的重心的轨迹方程是
.
13.设向量a与b的夹角为θ,a = (3,3),2b-a = (-1,1),则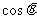 = .
= .
12.等比数列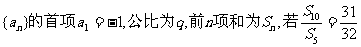 ,则q = ,
,则q = ,
Sn = .
11.已知一个半径为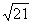 的球中有一个各条棱长相等的内接正三棱柱,则这下正三棱柱的棱长是
.
的球中有一个各条棱长相等的内接正三棱柱,则这下正三棱柱的棱长是
.
9.某校为了了解高三年级学生的视力状况,按男生和女生分层抽样,从全部600名学生中抽取60名进行检查,在抽取的学生中有男生36名,则高三年级中共有 女生.
|
 =
.
=
.8.已知抛物线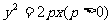 的焦点恰好是椭圆
的焦点恰好是椭圆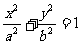 的右焦点F,且这两条曲线交点的连线过点F,则该椭圆的离心率为 ( )
的右焦点F,且这两条曲线交点的连线过点F,则该椭圆的离心率为 ( )
A.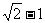 B.
B.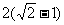 C.
C.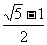 D.
D.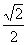
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com