
(1)复数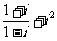 的值是
的值是
(A)0 (B)1 (C) -1 (D)1
(2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是
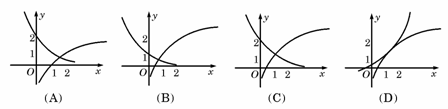
(3)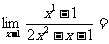
(A)0
(B)1
(C)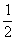 (D)
(D)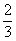
(4)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是
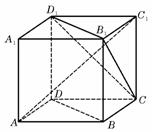 (A)BD∥平面CB1D1
(A)BD∥平面CB1D1
(B)AC1⊥BD
(C)AC1⊥平面CB1D1
(D)异面直线AD与CB1角为60°
(5)如果双曲线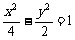 上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
(A)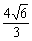 (B)
(B)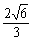 (C)
(C)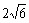 (D)
(D)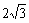
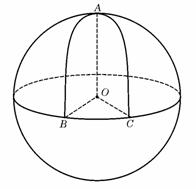 (6)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是
(6)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是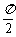 ,且三面角B-OA-C的大小为
,且三面角B-OA-C的大小为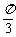 ,则从A点沿球面经B、C两点再回到A点的最短距离是
,则从A点沿球面经B、C两点再回到A点的最短距离是
(A)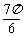 (B)
(B)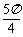
(C)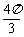 (D)
(D)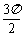
(7)设A{a,1},B{2,b},C{4,5},为坐标平面上三点,O为坐标原点,若 上的投影相同,则a与b满足的关系式为
上的投影相同,则a与b满足的关系式为
(A)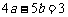 (B)
(B)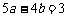
(C)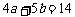 (D)
(D)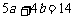
(8)已知抛物线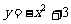 上存在关于直线
上存在关于直线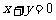 对称的相异两点A、B,则|AB|等于
对称的相异两点A、B,则|AB|等于
(A)3 (B)4 (C)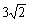 (D)
(D)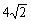
(9)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的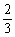 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为
(A)36万元 (B)31.2万元 (C)30.4万元 (D)24万元
(10)用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有
(A)288个 (B)240个 (C)144个 (D)126个
(11)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1, l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是
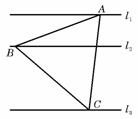 (A)
(A)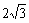 (B)
(B)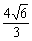
(C)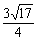 (D)
(D)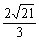
(12)已知一组抛物线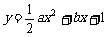 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
(A)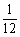 (B)
(B)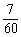 (C)
(C)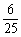 (D)
(D)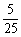
22.(本小题满分14分)
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n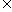 N *),其中x1为正实数.
N *),其中x1为正实数.
(Ⅰ)用xn表示xn+1;
(Ⅱ)若x1=4,记a4 =lg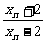 ,证明数列{an}成等比数列,并求数列{xn}的通
,证明数列{an}成等比数列,并求数列{xn}的通
项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
21.(本小题满分12分)
求F1、F2分别是椭圆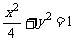 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是第一象限内该数轴上的一点,其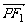 ·
·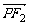 =-
=-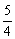 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
20.(本小题满分12分)
设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1, f(1))处的切线与直线x-6y-7=0垂直,导函数f'(x)的最小值为-12.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调递增区间,并求函数f(x)在[-1,3]上的最大值和最小值.
19.(本小题满分12分)
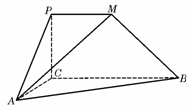 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的大小;
(Ⅲ)求多面体PMABC的体积.
18.(本小题满分12分)
已知cosα=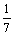 ,cos(α-β)=
,cos(α-β)=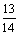 ,且0<β<α<
,且0<β<α<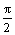 ,
,
(Ⅰ)求tan2α的值;
(Ⅱ)求β.
17.(本小题满分12分)
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否验收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4种进行检验,求至少有1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,来进行检验,只有2件产品合格时才接收这些产品,否则拒收,分别求出该商家检验出不合格产品为1件和2件的概率,并求该商家拒收这些产品的概率。
16.下面有五个命题:
①函数y=sin4x-cos4x,的最小正周期是π.
②终边在y轴上的角的集合是{a|α=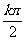 ,k∈Z}
,k∈Z}
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数y=3sin(2x+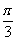 )的图象向右平移
)的图象向右平移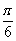 得到y=3 sin2x的图象.
得到y=3 sin2x的图象.
⑤角θ为第一象限角的充要条件是sinθ>0.
其中,真命题的编号是 (写出所有真命题的编号).
15.已知⊙O的方程是x2+y2-2=0, ⊙O′ 的方程是x2+y2-8x+10=0.由动点P内⊙O和⊙O′所引的切线长相等,则动点P的轨迹方程是 .
14.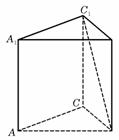 如图,在正三棱柱ABC-A1B1C1中,侧棱长为
如图,在正三棱柱ABC-A1B1C1中,侧棱长为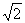 ,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是
.
,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com