
21.(本小题满分12分)
已知数列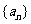 ,
,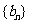 与函数
与函数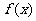 ,
,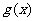 ,
,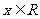 满足条件:
满足条件:
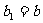 ,
,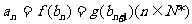 .
.
(I)若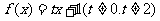 ,
,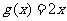 ,
,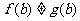 ,
,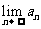 存在,求
存在,求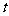 的取值范围;并求
的取值范围;并求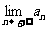 (用
(用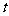 表示)
表示)
(II)若函数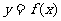 为
为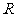 上的增函数,
上的增函数,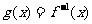 ,
,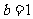 ,
,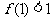 ,证明对任意
,证明对任意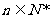 ,
,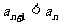 .
.
20.(本小题满分14分)
已知正三角形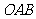 的三个顶点都在抛物线
的三个顶点都在抛物线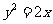 上,其中
上,其中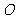 为坐标原点,设圆
为坐标原点,设圆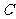 是
是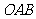 的外接圆(点
的外接圆(点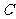 为圆心)
为圆心)
(I)求圆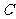 的方程;
的方程;
(II)设圆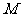 的方程为
的方程为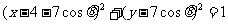 ,过圆
,过圆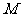 上任意一点
上任意一点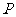 分别作圆
分别作圆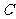 的两条切线
的两条切线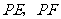 ,切点为
,切点为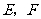 ,求
,求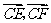 的最大值和最小值.
的最大值和最小值.
19.(本小题满分12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本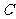 与产量
与产量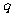 的函数关系式为
的函数关系式为
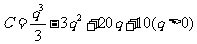
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格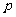 与产量
与产量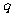 的函数关系式如下表所示:
的函数关系式如下表所示:
|
市场情形 |
概率 |
价格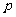 与产量 与产量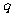 的函数关系式 的函数关系式 |
|
好 |
0.4 |
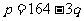 |
|
中 |
0.4 |
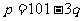 |
|
差 |
0.2 |
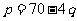 |
设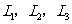 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量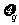 ,表示当产量为
,表示当产量为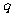 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润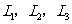 与产量
与产量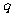 的函数关系式;
的函数关系式;
(II)当产量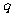 确定时,求期望
确定时,求期望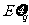 ;
;
(III)试问产量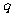 取何值时,
取何值时,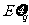 取得最大值.
取得最大值.
18.(本小题满分12分)
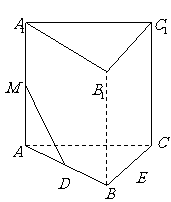
如图,在直三棱柱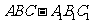 中,
中,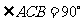 ,
,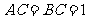 ,
,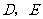 分别为棱
分别为棱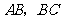 的中点,
的中点,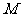 为棱
为棱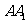 上的点,二面角
上的点,二面角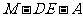 为
为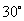 .
.
(I)证明: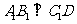 ;
;
(II)求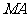 的长,并求点
的长,并求点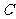 到平面
到平面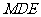 的距离.
的距离.

17.(本小题满分12分)
已知函数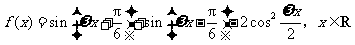 (其中
(其中 )
)
(I)求函数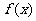 的值域;
的值域;
(II)若对任意的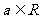 ,函数
,函数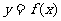 ,
,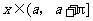 的图象与直线
的图象与直线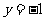 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定 的值(不必证明),并求函数
的值(不必证明),并求函数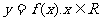 的单调增区间.
的单调增区间.
16.将数字1,2,3,4,5,6拼成一列,记第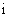 个数为
个数为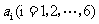 ,若
,若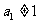 ,
,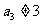 ,
,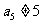 ,
,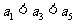 ,则不同的排列方法有 种(用数字作答).
,则不同的排列方法有 种(用数字作答).
15.若一个底面边长为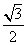 ,棱长为
,棱长为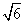 的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
14.设椭圆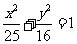 上一点
上一点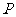 到左准线的距离为10,
到左准线的距离为10,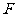 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点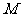 满足
满足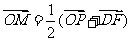 ,则
,则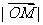 = .
= .
13.已知函数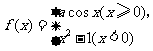 在点
在点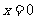 处连续,则
处连续,则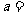 .
.
12.已知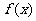 与
与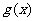 是定义在
是定义在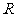 上的连续函数,如果
上的连续函数,如果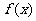 与
与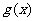 仅当
仅当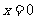 时的函数值为0,且
时的函数值为0,且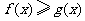 ,那么下列情形不可能出现的是( )
,那么下列情形不可能出现的是( )
A.0是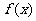 的极大值,也是
的极大值,也是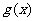 的极大值
的极大值
B.0是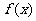 的极小值,也是
的极小值,也是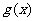 的极小值
的极小值
C.0是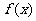 的极大值,但不是
的极大值,但不是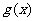 的极值
的极值
D.0是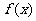 的极小值,但不是
的极小值,但不是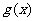 的极值
的极值
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com