
2.利用斜二测画法,一个平面图形的直观图是边长为1的正方形(如图),则这个平面图形的面积为 ( )
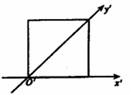
A.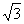 B.2 C.
B.2 C.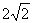 D.4
D.4
1.设I为全集,B∩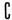 IA=B,则A∩B为 ( )
IA=B,则A∩B为 ( )
A.A B.B C.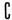 IB D.Φ
IB D.Φ
4。在正四棱柱ABCD-A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
 (3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?
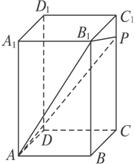
3.如图,在正四棱锥P-ABCD中,E是侧棱PB的中点,侧棱PA与底面ABCD所成角的正切值为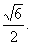
(I)求侧面PAD与底面ABCD所成的二面角的大小;
(II)求异面直线PD与AE所成角的正切值;
(III)在侧面PAD上寻找一点F,使EF⊥侧面PBC,
试确定点F的位置,并证明你找出的点F满足EF⊥侧面PBC.
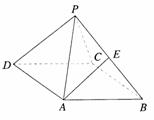
2.如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ADC为直角,AD∥BC,AB⊥AC,AB=AC=2,G为△PAC的重心,E为PB的中点,F在线段BC上,且CF=2FB.
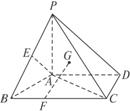
(1)求证:FG∥平面PAB;
(2)求证:FG⊥AC;
(3)当二面角P-CD-A多大时,FG⊥平面AEC?
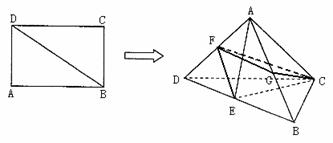
1.已知矩形ABCD中,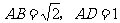 ,将ΔABD沿BD折起,使点A在平面BCD内的射影落在DC上,E、F、G分别为棱BD、AD、AB的中点。
,将ΔABD沿BD折起,使点A在平面BCD内的射影落在DC上,E、F、G分别为棱BD、AD、AB的中点。
(I)求证:DA⊥平面ABC;
(II)求点C到平面ABD的距离;(III)求二面角G-FC-E的大小。
20.(本题12分)设 轴、
轴、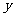 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是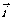 、
、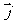 ,坐标平面上点
,坐标平面上点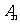 、
、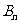
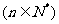 分别满足下列两个条件:①
分别满足下列两个条件:①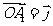 且
且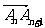 =
=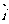 +
+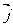 ;②
;②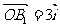 且
且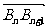 =
=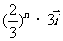 。(Ⅰ)求
。(Ⅰ)求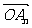 及
及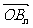 的坐标;
的坐标;
(Ⅱ)若四边形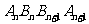 的面积是
的面积是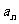 ,求
,求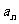
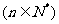 的表达式;
的表达式;
(Ⅲ)对于(Ⅱ)中的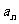 ,是否存在最小的自然数M,对一切
,是否存在最小的自然数M,对一切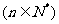 都有
都有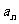 <M成立?若存在,求M;若不存在,说明理由.
<M成立?若存在,求M;若不存在,说明理由.
19.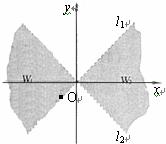 (本题12分)(05年北京)如图,直线l1:
(本题12分)(05年北京)如图,直线l1: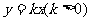 与直线l2:
与直线l2: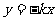 之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
(Ⅰ)分别用不等式组表示W1和W2;
(Ⅱ)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点. 求证△OM1M2的重心与△OM3M4的重心重合.
(17).(本题满分10分)(05年全国Ⅰ)设函数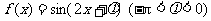 。y=f(x)图像的一条对称轴是直线
。y=f(x)图像的一条对称轴是直线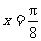 . (Ⅰ)求
. (Ⅰ)求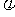 ;
;
(Ⅱ)求函数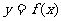 的单调增区间;
的单调增区间;
(Ⅲ)证明直线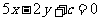 于函数
于函数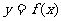 的图像不相切.
的图像不相切.
18.(本题12分)某人玩硬币走跳棋的游戏,已知硬币出现正、反面的概率都是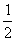 .棋盘上标有第0站、第1站、第2站、……、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
.棋盘上标有第0站、第1站、第2站、……、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为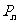 .
.
(I)求P0,Pl,P2;(II)求证: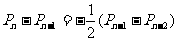
(Ⅲ)求玩该游戏获胜的概率.
16. (06年安徽卷)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面
(06年安徽卷)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面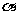 内,其余顶点在
内,其余顶点在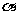 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到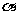 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面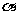 的距离可能是:①3; ②4; ③5; ④6; ⑤7
的距离可能是:①3; ②4; ③5; ④6; ⑤7
以上结论正确的为______________。(写出所有正确结论的编号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com