
18.(本小题满分12分)
已知复数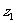 ,满足
,满足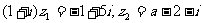 ,其中i为虚数单位,
,其中i为虚数单位,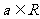 ,若
,若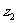 的共轭复数记为
的共轭复数记为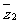 ,且
,且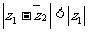 ,求
,求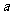 的取值范围.
的取值范围.
17.(本小题满分12分)
一架飞机载有乘客89人,在一次飞行中遇到了恶劣的气候条件,其中晕机的男乘客有24人,女乘客有8人;不晕机男乘客有31人,女乘客有26人.
(I)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断在恶劣气候条件下,男乘客是否比女乘客更容易晕机?请用统计学的有关知识,说明理由.
16.类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列一些性质:
①各棱长相等,同一顶点上的任两条棱的夹角相等;
②各个面是全等的正三角形,相邻两个面所成的二面角相等;
③各个面都是全等的正三角形,同一顶点的任何两条棱的夹角都相等
你认为比较恰当的是______________(把你认为正确的命题都写上).
15.若函数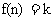 ,其中
,其中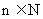 ,k是
,k是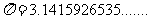 的小数点后第n位数字,例如
的小数点后第n位数字,例如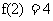 ,
,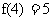 ,则
,则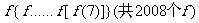 =__________
=__________
14.如果复数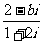 的实部和虚部互为相反数,那么实数b的值为_________.
的实部和虚部互为相反数,那么实数b的值为_________.
13.已知一个物体的运动方程是 ,其中S的单位是米,t的单位是秒,那么该物体在2秒末的瞬时速度是________米/秒。
,其中S的单位是米,t的单位是秒,那么该物体在2秒末的瞬时速度是________米/秒。
(1)分析法是从要证明的结论出发,逐步寻求使结论成立的
(A)充分条件 (B)必要条件 (C)充要条件 (D)等价条件
(2)曲线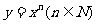 在
在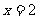 处的导数为12,则
处的导数为12,则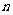 =
=
(A)1 (B)2 (C)3 (0)4
(3)事件A、B是相互独立的,下列四个式子:
①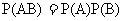 ②
②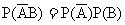
③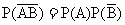 ④
④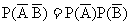 其中正确的有
其中正确的有
(A)1个 (B)2个 (C)3个 (D)4个
(4)下列几种推理过程是演绎推理的是
(A)某校高三1班55人,2班54人,3班52人,由此得高三所有班人数超过50人
(B)两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则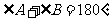
(C)由圆的圆长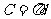 推测球的表面积
推测球的表面积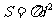
(D)在数列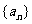 中,
中,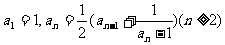 ,由此归纳出
,由此归纳出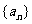 的通项公式
的通项公式
(5)满足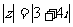 的复数z在复平面上对应的点的轨迹是
的复数z在复平面上对应的点的轨迹是
(A)一条直线 (B)圆 (C)两条直线 (D)椭圆
(6)下列关于工序流程图的说法正确的是
(A)流程图内每一道工序,可以用矩形框表示也可用平行四边形表示
(B)流程线是一条标有箭头的线段,可以是单向的也可以是双向的
(C)流程图中每一道工序是不可以再分的
(D)在工序流程图上不允许出现几道工序首尾相接的圈图或循环回路
(7)设两个变量x和y之间具有线性相关关系,它们的相关系数是r, y关于x的回归直线的回归系数为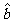 ,回归截距是
,回归截距是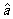 ,那么必有
,那么必有
(A) 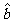 与r的符号相同 (B)
与r的符号相同 (B) 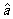 与r的符号相同
与r的符号相同
(C) 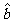 与r的符号相反 (D)
与r的符号相反 (D) 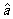 与r的符号相反
与r的符号相反
(8)在复平面上,复数i,1,4+2i所对应的点分别是A、B、C,则平行四边形ABCD的对角线BD的长为
(A)5 (B)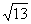 (C)
(C) 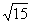 (D)
(D) 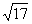
(9)函数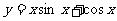 在下列哪个区间内是增函数
在下列哪个区间内是增函数
(A)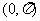 (B)
(B)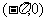 (C)
(C)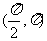 (D)
(D)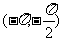
(10)已知函数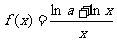 在(1,+∞)上为减函数,则
在(1,+∞)上为减函数,则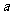 的取值范围为
的取值范围为
(A)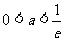 (B)
(B)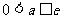
(C)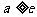 (D)
(D)
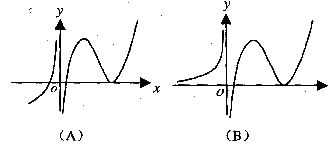
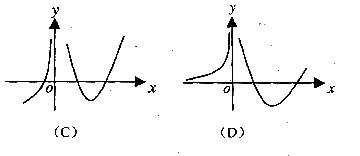
(11)设函数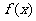 在定义域内可导,
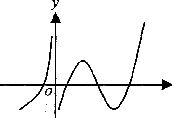
在定义域内可导,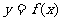 的图象如下图所示,则
的图象如下图所示,则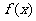 的导数
的导数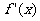 的图象大致为
的图象大致为
(12)对于R上可导的任意函数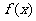 满足
满足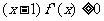 ,则必有
,则必有
(A)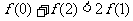 (B)
(B)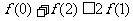
(C)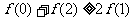 (D)
(D)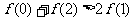
2006-2007学年度潍坊市高密第二学期期中检测高二考试
数学试题(文史类)
第Ⅱ卷(非选择题,共90分)
(17)(本小题满分12分)
设角 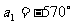 ,
,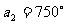 ,
,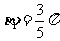 ,
,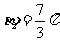 .
.
(Ⅰ)将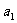 、
、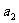 用弧度制表示出来,并指出它们各自所在的象限;
用弧度制表示出来,并指出它们各自所在的象限;
(Ⅱ)将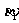 、
、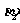 用角度制表示出来,并在
用角度制表示出来,并在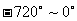 之间找出与它们有相同终边的所有角.
之间找出与它们有相同终边的所有角.
(18)(本小题满分12分)
袋子中有红、黄、白3种颜色的球各1个,从中每次任取一个,有放回地抽取3次求:
(Ⅰ)一个球全是红球的概率;
(Ⅱ)3个球颜色不全相同的概率;
(Ⅲ)3个球颜色全不相同的概率.
(19)(本小题满分12分)
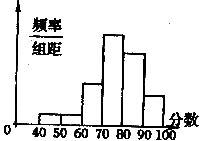
从某校参加数学竞赛的试卷中,抽出一个样本来考察竞赛的成绩分布,将样本分成6组,绘成频率分布直方图,从左到右各小组的小矩形的高的比为1:1:3:6:4:2,最右边的一组的频数是8,请结合直方图的信息,解答下列问题:
(Ⅰ)样本容量是多少?
(Ⅱ)成绩落在哪个范围的人数最多?人数是多少?
(Ⅲ)估计这次竞赛中,成绩高于70分的学生占总人数的百分率?
(20)(本小题满分12分)
已知两圆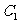 ︰
︰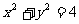 ,
,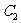 ︰
︰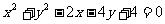 ,直线
,直线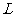 ︰
︰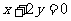 ,求经过圆C1和C2交点且和直线L相切的圆的方程。
,求经过圆C1和C2交点且和直线L相切的圆的方程。
(21)(本小题满分12分)
修订后的《中华人民共和国个人所得税》法规定,公民全月工资、薪金所得税的起征点为1600元,即月收入不超过1600元,免于征税;超过1600元的按以下税率纳税:超过部分在500元以内(含500元),税率为5%,超过500元至2000元的部分(含2000元),税率为10%,超过2000元至5000元部分,税率为15%,已知某厂工人的收入不高入3500元.
(Ⅰ)请用数学语言写出该厂工人的月收入与应纳税款的一个算法(不要写成程序框图或计算机程序);
(Ⅱ)将该算法用程序框图描述之.
(22)(本小题满分14分)
设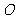 为坐标原点,曲线
为坐标原点,曲线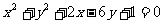 上有两点
上有两点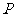 ,
,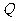 满足关于直线
满足关于直线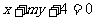 对称,又满足
对称,又满足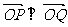 .
.
(Ⅰ)求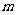 的值;
的值;
(Ⅱ)求直线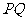 的方程
的方程
(13)某校共有2500名学生,其中男生1300名,女生1200名,用分层抽样的办法抽取了一个容量为200的样本,则男生应抽取_______名.
(14)已知扇形的周长是20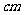 ,则扇形的圆心角为_______弧度时,扇形的面积最大,且面 积的最大值是_________.
,则扇形的圆心角为_______弧度时,扇形的面积最大,且面 积的最大值是_________.
(15)一个样本方差是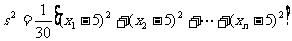 ,则这组数据的总和等于_____________.
,则这组数据的总和等于_____________.
(16)设点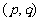 ,在
,在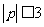 ,
,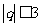 中按均匀分布出现,则方程
中按均匀分布出现,则方程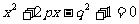 的两根都是实数的概率是_____________.
的两根都是实数的概率是_____________.
(1)甲、乙两人下棋,甲获胜的概率为0.4,甲不输的概率为0.9,则甲、乙两人下不成和棋的概率是
0.(A)0.5 (B)4 (C)0.3 (D)0.1
(2)甲、乙、丙、丁四名射手在选拔赛中所得的平均环数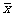 及方差
及方差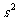 如下表所示,
如下表所示,
|
|
甲 |
乙 |
丙 |
丁 |
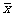 |
8 |
9 |
9 |
7 |
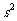 |
5.3 |
5.3 |
6 |
8.7 |
则选送决赛的最佳人选为
(A)甲 (B)乙 (C)丙 (D)丁
(3)用“辗转相除法”求得459和357的最大公约数为
(A)3 (B)9 (C)17 (D)51
(4)已知直线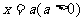 和圆
和圆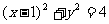 相切,则
相切,则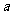 的值为
的值为
(A)5 (B)4 (C)3 (D)2
(5)某产品的废品率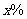 和每吨产品成本
和每吨产品成本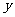 (元)之间的回归直线方程为
(元)之间的回归直线方程为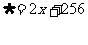 ,表明
,表明
(A)废品率每增加1%,成本增加256
(B)废品率每增加1%,产品每吨成本平均增加2元
(C)废品率每增加1%,成本增加2元
(D)废品率不变,产品成本为256元
(6) 设角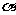 的终边过点
的终边过点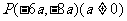 ,则
,则 的值是
的值是
(A)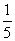 (B)
(B) (C)
(C) (D)
(D)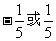
(7)一束光线自点P(1,2,1)发出经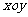 平面反射到点Q(3,3,6)后被吸收,那么所走过的路程是
平面反射到点Q(3,3,6)后被吸收,那么所走过的路程是
(A)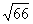 (B)
(B)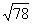
(C)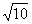 (D)
(D)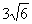
(8)同时抛两枚骰子,朝上的点数之和为奇数的概率是
(A)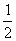 (B)
(B)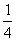
(C)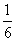 (D)
(D)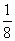
(9)圆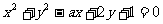 关于直线
关于直线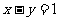 对称的圆为
对称的圆为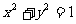 ,则实数
,则实数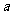 的值为
的值为
(A) (B)
(B)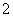 (C)
(C)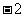 (D)
(D)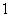
(10)右图给出的是计算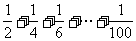 的值的一个程序框图,其中判断框内应填入的条件是
的值的一个程序框图,其中判断框内应填入的条件是
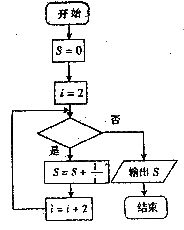
(A)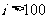 (B)
(B)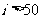 (C)
(C)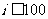 (D)
(D)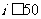
(11)在一个棱长为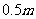 的正方体中盛满水,水中有一小虫在自由移动,从中随机取出
的正方体中盛满水,水中有一小虫在自由移动,从中随机取出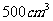 的水,则小虫被取出的概率为
的水,则小虫被取出的概率为
(A)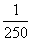 (B)
(B)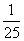 (C)
(C)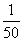 (D)
(D)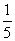
(12)若圆 始终平分圆
始终平分圆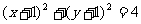 的周长,则
的周长,则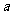 、
、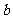 应满足的关系式是
应满足的关系式是
(A)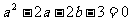 (B)
(B)
(C)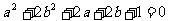 (D)
(D)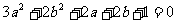
第Ⅱ卷(非选择题共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com