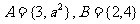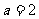2．若集合，则“”是“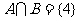”的 (　　 )

　　　 A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

1．在复平面内，复数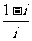对应的点位于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．第一象限　　　　　　 B．第二象限　　　　　　 C．第三象限　　　　　　 D．第四象限

20．(本小题共14分)

已知数列{a_n}中，前n项和为S_n，点(a_n+1，S_n+1)在直线y=4x－2，其中n=1，2，3……，

　 (Ⅰ)设b_n=a_n+1－2a_n，且a₁=1，求证数列{b_n}是等比数列；

　 (Ⅱ)令f(x)=b₁x+b₂x²+…+b_nxⁿ，求函数f(x)在点x=1处的导数f′(1)并比较f′(1)与

6n²－3n的大小.

19．(本小题共13分)

　　 已知双曲线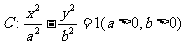的离心率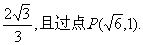

　 (Ⅰ)求双曲线C的方程；

　 (Ⅱ)若直线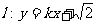与双曲线C恒有两个不同的交点A和B，且，

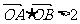求k的取值范围.

18．(本小题共13分)

经统计，某校教工食堂一个售饭窗口每天中午排队买饭的教工人数及相应的概率如下：

　 (Ⅰ)每天中午不超过20位教工排队买饭的概率是多少？

　 (Ⅱ)一周5个工作日中，若有3天或3天以上中午出现超过15位教工排队买饭的概率

大于0.80，学校就需要增加售饭窗口，请问该学校是否需要增加售饭窗口？

17．(本小题共14分)

　 如图，已知三棱锥P-ABC中，PA⊥平面ABC，AN⊥BC于N，D是AB的中点，且PA=1，AN=BN=CN=.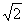

　 (Ⅰ)求证：PB⊥AC；

　 (Ⅱ)求异面直线CD与PB所成角的大小；

　 (Ⅲ)求点A到平面PBC的距离.

16．(本小题共13分)

　　　　 △ABC的三个内角A，B，C所对的边分别是a，b，c，向量m=(sinB，1－cosB)， n=(sinB，cosB)，且m·n=0.

　 (Ⅰ)求cosB的值；

　 (Ⅱ)求证：b²≥3ac.

15．(本小题共13分)

已知函数f(x)=x³－2ax²+6bx的图象与直线15x+y－4=0相切，切点为(1，－11).

　 (Ⅰ)求a，b的值；

　 (Ⅱ)求函数f(x)的单调递减区间.

14．定义一种运算“*”，它对于整数n满足以下运算性质：

　 (1)2*1001=1；(2)(2n+2)*1001=3·[(2n)*1001]，则2008*1001的值是　　　 　.

13．已知x,y满足条件y的最大值为8，则k=　　 .