
3.已知函数 处取得最小值,则函数
处取得最小值,则函数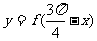 是 ( )
是 ( )
A.偶函数且它的图象关于点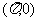 对称
对称
B.偶函数且它的图象关于点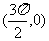 对称
对称
C.奇函数且它的图象关于点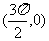 对称
对称
D.奇函数且它的图象关于点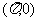 对称
对称
2.已知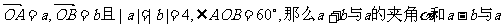 的夹角
的夹角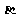 分别为 ( )
分别为 ( )
A.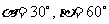 B.
B.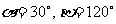
C.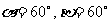 D.
D.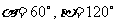
1.已知集合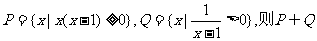 ,等于 ( )
,等于 ( )
A.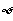 B.
B.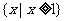 C.
C.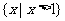 D.
D.
22.(本小题满分14分)
定义在实数集上的高次函数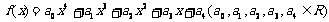 ,当
,当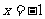 时,
时,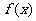 取极大值
取极大值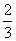 ,且函数
,且函数 的图象关于点
的图象关于点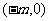 对称.
对称.
(1)求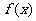 的表达式;
的表达式;
(2)试在函数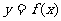 图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在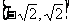 上;
上;
(3)(理科必做,文科选做)
设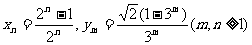 ,求使
,求使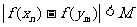 成立的最小正整数M的值.
成立的最小正整数M的值.
21.(本小题满分12分)
学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费为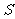 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为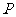 元,
元, ,
, ;其中
;其中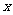 为每吨煤的价格(单位:元),
为每吨煤的价格(单位:元),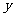 为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格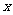 表示为每百度电价
表示为每百度电价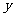 的函数;
的函数;
(2)如果每百度电价不低于60元,则用煤烧水时每吨煤的最高价格是多少?
20.(本小题满分12分)
函数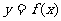 是定义在
是定义在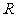 上的偶函数,且对任意实数
上的偶函数,且对任意实数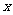 ,都有
,都有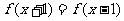 成立。已知当
成立。已知当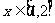 时,
时,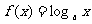
(1)求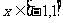 时,函数
时,函数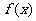 的解析式;
的解析式;
(2)求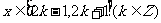 时,函数
时,函数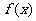 的解析式;
的解析式;
(3)若函数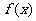 的最大值为
的最大值为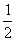 ,在区间
,在区间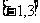 上,解关于
上,解关于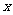 的不等式
的不等式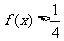
19.(本小题满分12分)
设a为实数,函数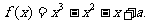
(Ⅰ)求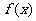 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线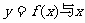 轴仅有一个交点.
轴仅有一个交点.
18.(本小题满分12分)
设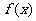 是定义在R上的函数,对
是定义在R上的函数,对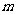 、
、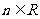 恒有
恒有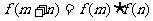 ,且当
,且当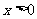 时,
时,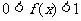 。
。
求证:
(1)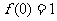 ;
;
(2)证明: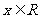 时恒有
时恒有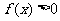 ;
;
(3)求证: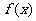 在R上是减函数;
在R上是减函数;
17.(本小题满分12分)
二次函数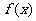 满足
满足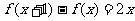 ,且
,且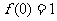 ,
,
(1)求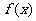 的解析式;
的解析式;
(2)在区间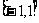 上
上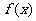 的图象恒在
的图象恒在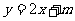 的图象上方,试确定实数
的图象上方,试确定实数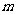 的范围.
的范围.
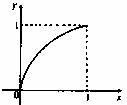
16.已知定义在区间[0,1]上的函数y=f(x),图象如图所示.对满足0<x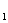 <x
<x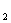 <1的任意x
<1的任意x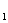 ,x
,x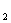 ,给出下列结论:
,给出下列结论:
①
f(x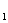 )-f(x
)-f(x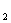 )>x
)>x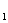 -x
-x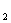 ;
;
②
x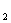 f(x
f(x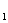 )>x
)>x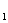 f(x
f(x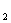 );
);
③
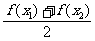 <f(
<f(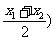 .
.
其中正确结论的序号是____________(把所有正确结论的序号都填上).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com