2．若

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

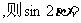
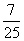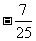　　　 A．　　　　　　　　　　 B．　　　　　　　　 C．1　　　　　　　　　　　　 D．－1

1．设P、Q是两个非空集合,定义集合间的一种运算“⊙”:P⊙Q =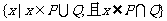，如果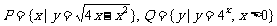，则P⊙Q 等于　　 (　　 )

　　　 A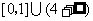．　 B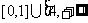．　　 C．[1，4]　　　　　　　　 D．(4，+∞)

22．函数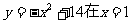处的切线方程为l，点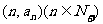都在直线l上，数列{a_n}的前n项和为S_n，数列{b_n}满足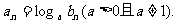

　 (1)试判断是否存在自然数M，使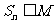恒成立，若存在，求出相应的M的最小值；若不存在，请说明理由；

　 (2)是否存在自然数N，使得当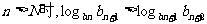恒成立，若存在，求出相应的N的最小值，若不存在，请说明理由；

　 (3)若的大小，并说明理由.

21．某商场预计全年分批购入每台价值2000元的电视机共3600台，每批都购入x台(x

是正整数)，且每批均需付运费400元，储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比，若每批购入400台，则全年需用去运费和保管费共43600元，现在全年只有24000元资金可以用于支付这笔费用，请问：能否恰当的安排每批进货的数量，使资金够用？写出你的结论，并说明理由.

20．定义在R上的函数f(x)满足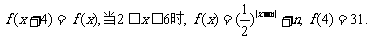

　 (1)求m，n的值；

　 (2)比较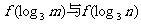的大小.

19．已知

　 (1)证明f(x)在(－1，1)上为奇函数；

　 (2)对数列；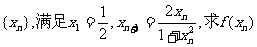

　 (3)求证

18．函数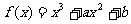的图象在点P(1，0)处的切线与直线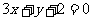平行.

　 (1)求a，b的值；

　 (2)求函数f(x)的单调区间；

　 (3)求函数f(x)在区间[0，t](t>0)上的最大值和最小值.

17．在△ABC中，三个内角A、B、C及其对边.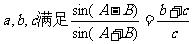

　 (1)求角A的大小；

　 (2)若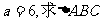的面积的最大值.

16．设函数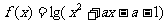，给出下述命题：

①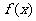有最小值；

②当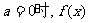的值域为;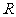

③若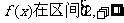上单调递增，则实数a的取值范围是

则其中正确的命题是　　　　 (要求：把正确命题的序号都填上).

15．已知，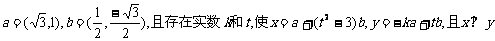

则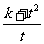的最小值为　　　　　 .