
3.将直线l:2x+3y-1=0,沿向量a =(-1,-2)平移后得到直线l′,则直线 l′的方程是( )
A. 2x+3y-7=0 B. 2x+3y-5=0 C.2x+3y-3=0 D. 2x+3y+7=0
2.cos(-3000)等于 ( )
A. -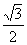 B.-
B.-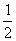 C.
C. 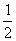 D.
D.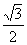
1.设全集U={1,3,5,7}则集合M满足
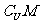 ={5,7},则集合M为 ( )
={5,7},则集合M为 ( )
A. 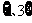 B.
B.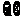 或
或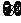 C.{1,3,5,7} D.
C.{1,3,5,7} D. 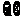 或
或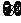 或
或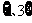
22.(12分)已知椭圆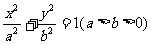 的离心率
的离心率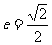 ,F1、F2为其左右焦点,点P为椭圆C上动点. △PF1F2面积的最大值为2.
,F1、F2为其左右焦点,点P为椭圆C上动点. △PF1F2面积的最大值为2.
(1)求椭圆C的方程;
(2)设椭圆C交x轴于A、B两点,M为椭圆内动点,满足 、
、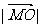 、
、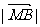 成等比数列,求
成等比数列,求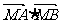 的取值范围.
的取值范围.
21.(12分)设双曲线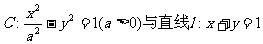 相交于不同的两点A、B.
相交于不同的两点A、B.
(1)求双曲线C的离心率e的取值范围;
(2)设直线l与y轴的交点为P,且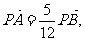 求a的值.
求a的值.
20.(12分)定义在R上的函数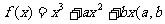 为常数),在x=-1处有极值,且
为常数),在x=-1处有极值,且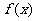 的图象在P(1,
的图象在P(1,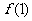 )处的切线平行于直线y=8x.
)处的切线平行于直线y=8x.
(1)求函数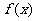 的解析式及极值;
的解析式及极值;
(2)对任意α、β∈R,求证
19.(12分)已知圆K过定点A(a,0)(a >0),圆心K在抛物线C: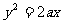 上运动,MN为圆K在y轴上截得的弦.
上运动,MN为圆K在y轴上截得的弦.
(1)求证:|MN|为定值;
(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆K有怎样的位置关系,并说明理由.
18.(12分)某电信服务点有连成一排的7座电话亭,此时全部空着,现有2位陌生人各随机选择不同的电话亭打电话.
(1)求这2个人选择的电话亭相隔数为3的概率;
(2)若电信管理员预言这2人之间至少相隔2座电话亭,求管理员预言为真的概率.
17.(10分)已知a<1,解关于x的不等式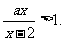
16.过原点引直线l与动圆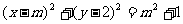 相切
相切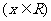 ,则切点M的轨迹方程为
.
,则切点M的轨迹方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com